一、单选题(本大题共8小题,每小题5分,共40分,每小题只有一个选项正确)
-
A .  B . 1
C . -1
D .
B . 1
C . -1
D . 
-
A . 1
B .  C . 2
D . 4
C . 2
D . 4
-
3.
(2021高二下·顺德月考)
某同学对如右图所示的小方格进行涂色一种颜色,若要求每行、每列中都恰好只涂一个方格,则不同的涂色种数为( )

A . 12
B . 36
C . 24
D . 48
-
-
A . 576
B . 432
C . 388
D . 216
-
6.
(2021高二下·顺德月考)
某地病毒爆发,全省支援,需要从我市某医院某科室的5名男医生(含一名主任医师)、4名女医生(含一名主任医师)中分别选派3名男医生和2名女医生,则在有一名主任医师被选派的条件下,两名主任医师都被选派的概率为( )
-
-
二、多选题(本题共4小题,每小题5分,全部选对得5分,有漏选得2分,有错选得0分)
三、填空题(本大题共4小题,每小题5分,共20分,其中第16题的第一个空3分,第二个空2分)
-
-
-
-
16.
(2021高二下·顺德月考)
若

,则

的值是
;在上述展开式右边的九项中,随机任取不同的三项,假设这三项均不相邻,则有
种不同的取法(用数字作答).
四、解答题(本题共6小题,其中17题10分,其余各题12分,解答题须写出文字说明或演算步骤)
-
-
(1)
求

的值;
-
(2)
求展开式中含

的项的系数.
-
-
(1)
若

是纯虚数,求实数

的值.
-
(2)
若复数

在复平面上对应的点在第二象限,且

,求实数

的取值范围.
-
19.
(2021高二下·顺德月考)
某用人单位在一次招聘考试中,考试卷上有

三道不同的题,现甲、乙两人同时去参加应聘考试,他们考相同的试卷已知甲考生对

三道题中的每一题能解出的概率都是

,乙考生对

三道题能解出的概率分别是

,

,

,且甲、乙两人解题互不干扰,各人对每道题是否能解出是相互独立的.
-
-
(2)
设

表示乙在考试中能解出题的道数,求

的数学期望;
-
(3)
按照“考试中平均能解出题数多”的择优录取原则,如果甲、乙两人只能有一人被录取,你认为谁应该被录取,请说出理由.
-
20.
(2022高二下·玉林月考)
某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产

万件,需另投入流动成本

万元,当年产量小于

万件时,

(万元);当年产量不小于

万件时,

(万元).已知每件产品售价为

元,假若该同学生产的商品当年能全部售完.
-
(1)
写出年利润

(万元)关于年产量

(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
-
(2)
当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?(取

).
-
21.
(2021高二下·顺德月考)
2020年新冠疫情以来,医用口罩成为防疫的必需品.根据国家质量监督检验标准,过滤率是生产医用口罩的重要参考标准,对于直径小于5微米的颗粒的过滤率必须大于90%.为了监控某条医用口罩生产线的生产过程,检验员每天从该生产线上随机抽取10个医用口置,检测其过滤率,依据长期生产经验,可以认为这条生产线正常状态下生产的医用口罩的过滤率

服从正态分布

.假设生产状态正常,生产出的每个口罩彼此独立.记

表示一天内抽取10个口罩中过滤率小于或等于

的数量.
-
(1)
求

的概率;
-
(2)
求

的数学期望

;
-
-
-
-
(2)
设

,若

有三个不同的零点,求

的取值范围.

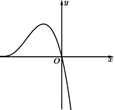 B .
B . 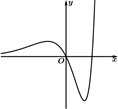 C .
C .  D .
D . 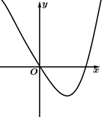

,则
,
,
,