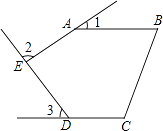
已知:如图,四边形 是平行四边形,对角线
、
相交于点
.

求证: ,
,嘉琪的证明过程如下:
| 证明:从四边形 ∴_____________________________ ∴ ∴ ∴ |
上面证明过程中,“________”应补充的步骤是( )
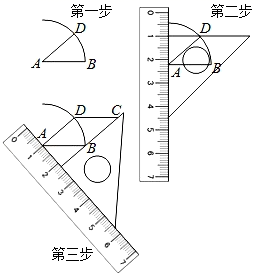
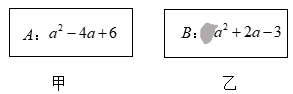
甲:若 ,则点P的个数为0;
乙:若 ,则点P的个数为1;
丙:若 ,则点P的个数为1.
下列判断正确的是( )

|
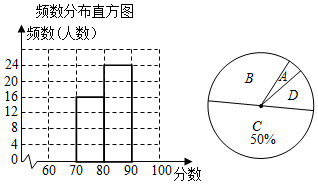
类别 |
分数段 |
频数(人数) |
|
A |
|
a |
|
B |
|
16 |
|
C |
|
24 |
|
D |
|
6 |
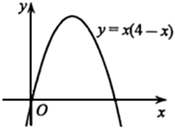
①若x=5,则每星期可卖出 ▲ 件,每星期的销售利润为 ▲ 元;
②当x为何值时,W最大,W的最大值是多少?
①写出W与y的函数关系式,并通过计算判断:当m=10时每星期销售利润能否达到(1)中W的最大值;
②若使y=10时,每星期的销售利润W最大,直接写出W的最大值为 ▲ .
①求 与
的函数关系式;
②求证: 平分
的面积;