 B .
B .  C .
C .  D .
D . 
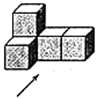
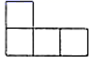 B .
B . 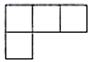 C .
C . 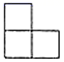 D .
D . 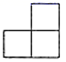

(Ⅰ)线段 的长等于;
(Ⅱ)以点 为旋转中心,将
绕点
旋转,点
,
的对应点分别是点
,
.当
的面积取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点
,
,并简要说明点
,
的位置是如何找到的(不要求证明).
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ▲ ;
(Ⅱ)解不等式②,得 ▲ ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 ▲ .
参考数据: ,
,
,
.

|
从 | 到达 | |
| 甲 | 5:00 |
|
| 乙 |
| 9:00 |
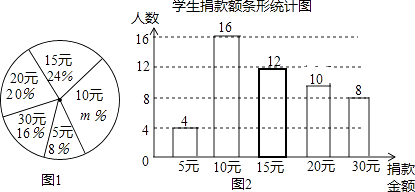
① ,
两城的距离为
;
②甲车的速度为 ,乙车的速度为
;
③乙车追上甲车用了 ,此时两车离开
城的距离是
;
④当9:00时,甲乙两车相距 ;
⑤当甲车离开 城
时,甲车行驶了
;
⑥当乙车出发行驶 时,甲乙两车相距
.
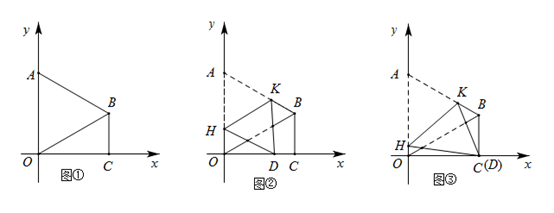
(Ⅰ)如图①,若点 坐标为
,求
的长;
(Ⅱ)如图②,将四边形 折叠,使点
落在线段
上的点为点
,
为折痕,点
在
上,点
在
上,且使
轴.
①试判断四边形 的形状,并证明你的结论;
②求 的值;
(Ⅲ)如图③,将四边形 折叠,使点
落在线段
上的点
与
点重合,
为折痕,点
在
上,点
在
上,求
的值(直接写出结果即可).
(Ⅰ)求 ,
两点的坐标;
(Ⅱ)若点 是抛物线上的点,点
的横坐标为
,过点
作
轴,垂足为
.线段
与直线
交于点
,当
时,求点
的坐标;
(Ⅲ)若点 是
轴上的点,且满足
,求点
的坐标.