
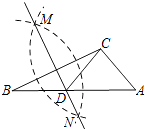
①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB的度数为( )




( 1 )将△ABC向下平移5个单位得到△A1B1C1 , 并写出点A1的坐标;
( 2 )画出△A1B1C1绕点C1逆时针旋转90°后得到的△A2B2C1 , 并写出点A2的坐标;.
( 3 )在(2)的条件下,求△A1B1C1在旋转过程中扫过的面积(结果保留π)

其中百丽宫观众的评分位于A组有14人,评分分别为:
10,10,9.8,9.8,9.7,9.6,9.6,9.5,9.5,9.4,9.2,9.2,9.2,9.2;
两家电影院观众评分的平均数,中位数,众数(单位:分)如表所示:
| 电影院 | 百丽宫 | UME |
| 平均数 | 9.2 | 9.2 |
| 中位数 | n | 9.5 |
| 众数 | 9.2 | 9.5 |
克罗狄斯·托勒密(约90年- 168 年),古希腊天文学家、地理学家和光学家,在数学方面,他还论证了四边形的特性,即有名的托勒密定理,托勒密定理的内容如下:
圆的内接四边形的两条对角线的乘积等于两组对边乘积的和,即:如图1,若四边形ABCD
内接于⊙O,则有
任务:

|
售价x (元/件) |
150 |
160 |
170 |
180 |
|
日销售量y (件) |
200 |
180 |
160 |
140 |
|
日销售纯利润w (元) |
8000 |
8800 |
9200 |
9200 |
另外,该网店每日的固定成本折算下来为2000元。
注:日销售纯利润=日销售量×(售价-进价)-每日固定成本
②该商品进价是元/件,当售价是元/件时,日销售纯利润最大,最大纯利润是元。


活动一:将图1中的纸片DEF沿AC方向平移,连接AE,BD(如图2),当点F与点C重合时停止平移。
[思考]图2中的四边形ABDE是平行四边形吗?请说明理由。
[发现]当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3)。求AF的长。
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转a度(0≤a≤90),连接OB,OE (如图4)。
[探究]当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由。