
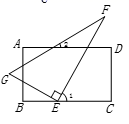

 B .
B . 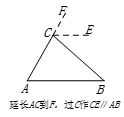 C .
C . 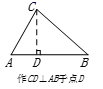 D .
D . 





①作出AB的垂直平分线MN , MN分别与AB交于点D , 与BC交于点E .
②过点B作BF垂直于AE , 垂足为F .

请认真阅读上述统计图,解决下列问题:
|
充电形式 |
充电费用 |
服务费 |
|
快充 |
0.8元/kW·h |
0.45元/ kW·h |
|
慢充 |
0.3元/kW·h |
0.45元/ kW·h |
出租车司机小李想用快充和慢充相结合的方式给自己的汽车充电,充电量为30kW·h,若要使此次充电的总费用不超过325元,则小李用快充形式最多充电多少kW·h?(注:充电总费用=充电费+服务费)
我们知道三角形外接圆的圆心叫做三角形的外心,三角形内切圆的圆心叫做三角形的内心.由于三角形的三条高(或高所在的直线)相交于一点,因此我们把三角形三条高的交点叫做三角形的垂心.下面我们以锐角三角形为例,证明三角形的三条高相交于一点.
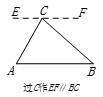
如图,在△ABC中,AD , BE分别是BC , AC边上的高,且AD与BE相交于点P . 连接CP并延长,交AB于点F .
求证:CF⊥AB .
证明:分别过点A , B , C作它们所对边的平行线,三条平行线两两相交于点M , N , Q . 分别连接PM , PN , PQ .
∵MN BC , MQ
AB , NQ
AC ,
∴四边形MABC , 四边形ANBC , 四边形ABQC都是平行四边形.
∴BC=AM=AN , AC=BN=BQ , AB=MC=CQ .
∵AD⊥BC ,
∴∠MAD=∠ADB=90°,即AD⊥MN .
∴PM=PN .
…
学习任务:


图1

图2
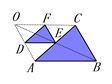
数学活动课上,老师让同学们结合下述情境,提出一个数学问题:如图1,四边形ABCD是正方形,四边形BEDF是矩形.

探究展示:
“兴趣小组”提出的问题是:“如图2,连接CE . 求证:AE⊥CE . ”并展示了如下的证明方法:
证明:如图3,分别连接AC , BD , EF , AF . 设AC与BD相交于点O .
∵四边形ABCD是正方形,
∴OA=OC= AC , OB=OD=
BD , 且AC=BD .
又∵四边形BEDF是矩形,
∴EF经过点O ,
∴OE=OF= EF , 且EF=BD .
∴OE=OF , OA=OC .
∴四边形AECF是平行四边形.(依据1)
∵AC=BD , EF=BD ,
∴AC=EF .
∴四边形AECF是矩形.(依据2)
∴∠CEA=90°,
即AE⊥CE .
上述证明过程中“依据1”“依据2”分别是什么?
“创新小组”受到“兴趣小组”的启发,提出的问题是:“如图4,分别延长AE , FB交于点P , 求证:EB=PB . ”请你帮助他们写出该问题的证明过程.
