福建省宁德市2021届高三数学三模试卷

更新时间：2021-06-25 浏览次数：95 类型：高考模拟

一、单选题

1. (2021·宁德模拟) 复平面内复数 $\text{[math]}$ ， $\text{[math]}$ 对应的点关于实轴对称，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . -25 D . 25

答案解析收藏纠错 + 选题
2. (2021·宁德模拟) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·宁德模拟) 不等式 $\text{[math]}$ 成立的一个充分不必要条件是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·宁德模拟) 如图，抛物线型太阳灶是利用太阳能辐射，通过聚光获取热量进行炊事烹饪食物的一种装置.由于太阳光基本上属于平行光线，所以当太阳灶(旋转抛物面)的主光轴指向太阳的时候，平行的太阳光线入射到旋转抛物面表面，经过反光材料的反射，这些反射光线都从它的焦点处通过，在这里形成太阳光线的高密集区，抛物面的焦点就在它的主光轴上.现有一抛物线型太阳灶，灶口直径 $\text{[math]}$ 为 $\text{[math]}$ ，灶深 $\text{[math]}$ 为 $\text{[math]}$ ，则焦点到灶底(抛物线的顶点)的距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·宁德模拟) 根据历年的气象数据，某市5月份发生中度雾霾的概率为0.25，刮四级以上大风的概率为0.4，既发生中度雾霾又刮四级以上大风的概率为0.2.则在发生中度雾霾的情况下，刮四级以上大风的概率为（）

A . 0.8 B . 0.625 C . 0.5 D . 0.1

答案解析收藏纠错 + 选题
6. (2021·宁德模拟) 如图，在直四棱柱 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别在棱 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 四点共面，则下列结论错误的是（）

A . 任意点P，都有 $\text{[math]}$ B . 任意点P，四边形 $\text{[math]}$ 不可能为平行四边形 C . 存在点P，使得 $\text{[math]}$ 为等腰直角三角形 D . 存在点P，使得 $\text{[math]}$ 平面 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·宁德模拟) 《周髀算经》是中国最古老的天文学､数学著作，公元3世纪初中国数学家赵爽创制了“勾股圆方图”(如图)，用以证明其中记载的勾股定理.现提供4种不同颜色给如图中5个区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，则不同涂色的方法种数为（）

A . 36 B . 48 C . 72 D . 96

答案解析收藏纠错 + 选题
8. (2021·宁德模拟) 已知函数 $\text{[math]}$ ，实数 $\text{[math]}$ ， $\text{[math]}$ 满足不等式 $\text{[math]}$ ，则下列不等式成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题

9. (2021·宁德模拟) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ 的夹角为 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·宁德模拟) 某校研究性学习小组根据某市居民人均消费支出的统计数据，制作2018年人均消费支出条形图（单位：元）和2019年人均消费支出饼图（如图）.已知2019年居民人均消费总支出比2018年居民人均消费总支出提高8.5%，则下列结论正确的是（）

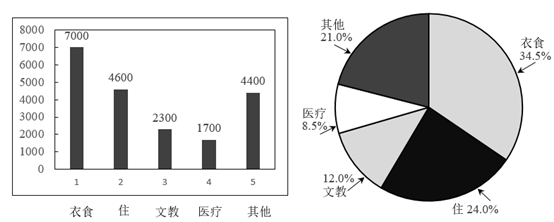
A . 2019年的人均衣食支出金额比2018年的人均衣食支出金额高 B . 2019年除医疗以外的人均消费支出金额等于2018年的人均消费总支出金额 C . 2019年的人均文教支出比例比2018年的人均文教支出比例有提高 D . 2019年人均各项消费支出中，“其他”消费支出的年增长率最低

答案解析收藏纠错 + 选题
11. (2021·宁德模拟) 已知函数 $\text{[math]}$ 的最小正周期为 $\text{[math]}$ ，则下列结论中正确的是（）

A . $\text{[math]}$ 对一切 $\text{[math]}$ 恒成立 B . $\text{[math]}$ 在区间 $\text{[math]}$ 上不单调 C . $\text{[math]}$ 在区间 $\text{[math]}$ 上恰有1个零点 D . 将函数 $\text{[math]}$ 的图像向左平移 $\text{[math]}$ 个单位长度，所得图像关于原点对称

答案解析收藏纠错 + 选题
12. (2021·宁德模拟) 已知正四棱锥的侧面积为 $\text{[math]}$ ，当该棱锥的体积最大时，以下结论正确的是（）

A . 棱锥的高与底面边长的比为 $\text{[math]}$ B . 侧棱与底面所成的角为 $\text{[math]}$ C . 棱锥的每一个侧面都是等边三角形 D . 棱锥的内切球的表面积为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题

13. (2021高三上·长沙开学考) 已知函数 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2021·宁德模拟) 能够说明“若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ”是假命题的一组整数 $\text{[math]}$ ， $\text{[math]}$ 的值依次为.

答案解析收藏纠错 + 选题
15. (2021·宁德模拟) 已知动点 $\text{[math]}$ 在圆 $\text{[math]}$ 上，双曲线 $\text{[math]}$ ： $\text{[math]}$ 的右焦点为 $\text{[math]}$ ，若 $\text{[math]}$ 的渐近线上存在点 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的离心率的取值范围是.

答案解析收藏纠错 + 选题
16. (2021·宁德模拟) 已知 $\text{[math]}$ 展开式中的所有项的系数和为64，则实数a=；展开式中常数项为.

答案解析收藏纠错 + 选题

四、解答题

17. (2021·宁德模拟) 在① $\text{[math]}$ ，② $\text{[math]}$ ， $\text{[math]}$ ，③ $\text{[math]}$ 这三个条件中任选一个，补充在下面的问题中，并解答问题.
已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ， ▲ ，数列 $\text{[math]}$ 满足 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2021·宁德模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的面积；
2. （2）在边 $\text{[math]}$ 上取一点 $\text{[math]}$ ，使得 $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2021·宁德模拟) 如图，在平面四边形 $\text{[math]}$ 中， $\text{[math]}$ 且 $\text{[math]}$ ，分别将 $\text{[math]}$ ､ $\text{[math]}$ 沿直线 $\text{[math]}$ 翻转为 $\text{[math]}$ ､ $\text{[math]}$ ( $\text{[math]}$ ， $\text{[math]}$ 不重合)，连结 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在平面 $\text{[math]}$ 内的正投影 $\text{[math]}$ 为 $\text{[math]}$ 的重心，求二面角 $\text{[math]}$ 的余弦值.
答案解析收藏纠错 + 选题
20. (2021·宁德模拟) 某同学利用假期到一超市参加社会实践活动，发现该超市出售种水果礼盒，每天进货一次，每销售1个水果盒可获利50元，卖不完的水果礼盒则需当天降价处理，每盒亏损10元.若每天该礼盒的需求量在 $\text{[math]}$ (单位：个)范围内等可能取值.
1. （1）求该礼盒的日需求量不低于15盒的概率；
2. （2）若某日超市进货13个水果礼盒，请写出该水果礼盒日销售利润 $\text{[math]}$ (元)的分布列，并求出 $\text{[math]}$ 的数学期望；
3. （3）这位同学想让水果礼盒的日销售利润最大，他应该建议超市日进货多少个水果礼盒？请说明理由.
答案解析收藏纠错 + 选题
21. (2021·宁德模拟) 已知 $\text{[math]}$ 、 $\text{[math]}$ 为椭圆 $\text{[math]}$ 的左、右顶点，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且直线 $\text{[math]}$ 、 $\text{[math]}$ 的斜率之积为 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的方程；
2. （2）直线 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ 、 $\text{[math]}$ 两点，直线 $\text{[math]}$ 、 $\text{[math]}$ 与直线 $\text{[math]}$ 分别交于 $\text{[math]}$ 、 $\text{[math]}$ ，线段 $\text{[math]}$ 的中点为 $\text{[math]}$ ，求证：直线 $\text{[math]}$ 的斜率为定值.
答案解析收藏纠错 + 选题
22. (2021·宁德模拟) 已知函数 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，讨论函数 $\text{[math]}$ 的单调性：
2. （2）若函数 $\text{[math]}$ 恰有两个极值点 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题