
① ;②
;③
;④
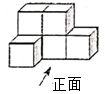
 B .
B .  C .
C . 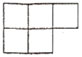 D .
D . 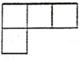

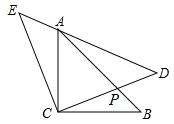
(收集数据)七年级20名学生测试成绩统计如下:
67,58,64,56,69,70,95,84,74,77,78,78,71,86,91,86,86,92,86,70
(整理数据)按照如下分数段整理、描述两组样本数据:
|
成绩 |
| | | | |
| 七年级 | 2 | 3 | 7 | 5 | 3 |
| 八年级 | 0 | 4 | 5 | 7 | 4 |
(分析数据)两组样本数据的平均数、中位数、众数、方差如下表所示:
| 年级 | 平均数 | 中位数 | 众数 | 方差 |
| 七年级 | 76.9 | | | 126.2 |
| 八年级 | 79.2 | 81 | 74 | 100.4 |
|
x/(元/件) |
22 |
25 |
30 |
35 |
… |
|
y/件 |
280 |
250 |
200 |
150 |
… |
在销售过程中销售单价不低于成本价,物价局规定每件商品的利润不得高于成本价的60%,
