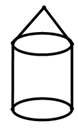
 B .
B .  C .
C . 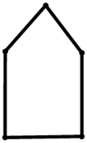 D .
D . 
 B .
B . 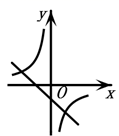 C .
C . 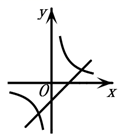 D .
D . 
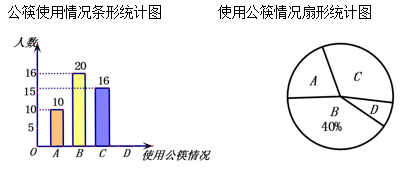
根据以上信息,解答下列问题:

如果函数 满足:对于自变量
取值范围内的任意
,
,
( 1 )若 ,都有
,则称
是增函数;
( 2 )若 ,都有
,则称
是减函数.
例题:证明函数 是增函数.
证明:任取 ,且
,
则
∵ 且
,
∴ ,
∴ ,即
,
∴函数 是增函数.
根据以上材料解答下列问题: