广西贵港市2021年中考数学试卷

更新时间：2024-07-13 浏览次数：292 类型：中考真卷

一、单选题

1. (2024七上·苏州期中) ﹣3的绝对值是（）

A . ﹣3 B . 3 C . - $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022八上·武江期末) 若分式 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是（）

A . x≠－5 B . x≠0 C . x≠5 D . x＞－5

答案解析收藏纠错 + 选题
3. (2024九下·广州模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . 2a－a＝1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·贵港) 一组数据8，7，8，6，4，9的中位数和平均数分别是（）

A . 7和8 B . 7.5和7 C . 7和7 D . 7和7.5

答案解析收藏纠错 + 选题
5. (2023八下·覃塘期末) 在平面直角坐标系中，若点P(a－3，1)与点Q(2，b＋1)关于x轴对称，则a＋b的值是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
6. (2023·新疆维吾尔自治区模拟) 不等式1＜2x－3＜x＋1的解集是（）

A . 1＜x＜2 B . 2＜x＜3 C . 2＜x＜4 D . 4＜x＜5

答案解析收藏纠错 + 选题
7. (2023九上·椒江月考) 已知关于x的一元二次方程x²－kx＋k－3＝0的两个实数根分别为 $\text{[math]}$ ，且 $\text{[math]}$ ，则k的值是（）

A . －2 B . 2 C . －1 D . 1

答案解析收藏纠错 + 选题
8. (2021·贵港) 下列命题是真命题的是（）

A . 同旁内角相等，两直线平行 B . 对角线相等的四边形是矩形 C . 对角线互相垂直的四边形是菱形 D . 两角分别相等的两个三角形相似

答案解析收藏纠错 + 选题
9. (2022·禄劝模拟) 某蔬菜种植基地2018年的蔬菜产量为800吨，2020年的蔬菜产量为968吨，设每年蔬菜产量的年平均增长率都为x，则年平均增长率x应满足的方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·德宏期末) 如图，点A，B，C，D均在⊙O上，直径AB＝4，点C是 $\text{[math]}$ 的中点，点D关于AB对称的点为E，若∠DCE＝100°，则弦CE的长是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
11. (2023九上·光明月考) 如图，在正方形ABCD中，E，F是对角线AC上的两点，且EF＝2AE＝2CF，连接DE并延长交AB于点M，连接DF并延长交BC于点N，连接MN，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2021·贵港) 如图，在 $\text{[math]}$ ABC中，∠ABC＝90°，AB＝8，BC＝12，D为AC边上的一个动点，连接BD，E为BD上的一个动点，连接AE，CE，当∠ABD＝∠BCE时，线段AE的最小值是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题

二、填空题

13. (2021·贵港) 甲、乙两人在相同条件下进行射击练习，每人10次射击战绩的平均数都是8环，方差分别为 $\text{[math]}$ ，则两人射击成绩比较稳定的是（填“甲”或“乙”）.

答案解析收藏纠错 + 选题
14. (2024九下·抚顺模拟) 第七次全国人口普查公布的我国总人口数约为1411780000人，将数据1411780000用科学记数法表示为.

答案解析收藏纠错 + 选题
15. (2023七下·鄠邑期末) 如图，AB∥CD，CB平分∠ECD，若∠B＝26°，则∠1的度数是.

答案解析收藏纠错 + 选题
16. (2022·玉州模拟) 如图，圆锥的高是4，它的侧面展开图是圆心角为120°的扇形，则圆锥的侧面积是.（结果保留 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
17. (2021·贵港) 如图，在矩形ABCD中，BD是对角线，AE⊥BD，垂足为E，连接CE，若 $\text{[math]}$ ，则tan∠DEC的值是.

答案解析收藏纠错 + 选题
18. (2021·贵港) 我们规定：若 $\text{[math]}$ ，则 $\text{[math]}$ .例如 $\text{[math]}$ ，则 $\text{[math]}$ .已知 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值是.

答案解析收藏纠错 + 选题

三、解答题

19. (2021·贵港)
1. （1）计算： $\text{[math]}$ ；
2. （2）解分式方程： $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. (2021·贵港) 尺规作图（只保留作图痕迹，不要求写出作法），如图，已知 $\text{[math]}$ ABC，且AB＞AC.

（ 1 ）在AB边上求作点D，使DB＝DC；

（ 2 ）在AC边上求作点E，使 $\text{[math]}$ ADE∽ $\text{[math]}$ ACB.

答案解析收藏纠错 + 选题
21. (2021·贵港) 如图，一次函数y＝x＋2的图象与反比例函数 $\text{[math]}$ 的图象相交，其中一个交点的横坐标是1.
1. （1）求k的值；
2. （2）若将一次函数y＝x＋2的图象向下平移4个单位长度，平移后所得到的图象与反比例函数 $\text{[math]}$ 的图象相交于A，B两点，求此时线段AB的长.
答案解析收藏纠错 + 选题

22. (2021·贵港) 某校为了了解本校学生每天课后进行体育锻炼的时间情况，在5月份某天随机抽取了若干名学生进行调查，调查发现学生每天课后进行体育锻炼的时间都不超过100分钟，现将调查结果绘制成如下两幅尚不完整的统计图表.请根统计图表提供的信息，解答下列问题：

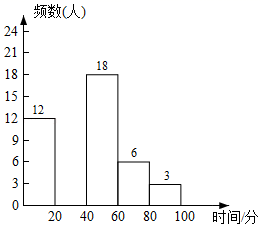
组别	锻炼时间（分）	频数（人）	百分比
A	0≤x≤20	12	20%
B	20＜x≤40	a	35%
C	40＜x≤60	18	b
D	60＜x≤80	6	10%
E	80＜x≤100	3	5%

（1）本次调查的样本容量是；表中a＝，b＝；
（2）将频数直方图补充完整；
（3）已知E组有2名男生和1名女生，从中随机抽取两名学生，恰好抽到1名男生和1名女生的概率是；
（4）若该校学生共有2200人，请根据以上调查结果估计：该校每天课后进行体育锻炼的时间超过60分钟的学生共有多少人？

答案解析收藏纠错 + 选题

23. (2022九下·沭阳模拟) 某公司需将一批材料运往工厂，计划租用甲、乙两种型号的货车，在每辆货车都满载的情况下，若租用30辆甲型货车和50辆乙型货车可装1500箱材料；若租用20辆甲型货车和60辆乙型货车可装载1400箱材料.
1. （1）甲、乙两种型号的货车每辆分别可装载多少箱材料？
2. （2）经初步估算，公司要运往工厂的这批材料不超过1245箱，计划租用甲、乙两种型号的货车共70辆，且乙型货车的数量不超过甲型货车数量的3倍，该公司一次性将这批材料运往工厂共有哪几种租车方案？
答案解析收藏纠错 + 选题
24. (2021·贵港) 如图，⊙O是 $\text{[math]}$ ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且∠DCF＝∠CAD.
1. （1）求证：CF是⊙O的切线；
2. （2）若cosB＝ $\text{[math]}$ ，AD＝2，求FD的长.
答案解析收藏纠错 + 选题
25. (2023·万山模拟) 如图，已知抛物线y＝ax²＋bx＋c与x轴相交于A(－3，0)，B两点，与y轴相交于点C(0，2)，对称轴是直线x＝－1，连接AC.
1. （1）求该抛物线的表达式；
2. （2）若过点B的直线l与抛物线相交于另一点D，当∠ABD＝∠BAC时，求直线l的表达式；
3. （3）在（2）的条件下，当点D在x轴下方时，连接AD，此时在y轴左侧的抛物线上存在点P，使 $\text{[math]}$ ，请直接写出所有符合条件的点P的坐标.
答案解析收藏纠错 + 选题
26. (2022·威海模拟) 已知在 $\text{[math]}$ ABC中，O为BC边的中点，连接AO，将 $\text{[math]}$ AOC绕点O顺时针方向旋转（旋转角为钝角），得到 $\text{[math]}$ EOF，连接AE，CF.
1. （1）如图1，当∠BAC＝90°且AB＝AC时，则AE与CF满足的数量关系是；
2. （2）如图2，当∠BAC＝90°且AB≠AC时，（1）中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；
3. （3）如图3，延长AO到点D，使OD＝OA，连接DE，当AO＝CF＝5，BC＝6时，求DE的长.
答案解析收藏纠错 + 选题