湖北省襄阳市南漳县2021年数学中考适应性考试试卷

更新时间：2024-07-13 浏览次数：94 类型：中考模拟

一、单选题

1. (2021九下·昭通期中) $\text{[math]}$ 的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·南漳模拟) 下列运算结果正确的是（）

A . a⁶÷a³＝a² B . （a²）³＝a⁵ C . 3a＋2a＝5a² D . a²－（－a）²＝0

答案解析收藏纠错 + 选题
3. (2021·南漳模拟) 下列四个几何体中，左视图与俯视图相同的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·南漳模拟) 不等式组 $\text{[math]}$ 的解集在数轴上可表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021·兴庆模拟) 如图，AB $\text{[math]}$ CD，AD⊥AC，∠BAD＝35°，则∠ACD＝（）

A . 35° B . 45° C . 55° D . 70°

答案解析收藏纠错 + 选题
6. (2021·南漳模拟) 参加一次绿色有机农产品交易会的每两家公司都签订了一份合同，所有公司共签订了45份合同，参加这次交易会的公司共有（）

A . 9家 B . 10家 C . 10家或9家 D . 19家

答案解析收藏纠错 + 选题
7. (2021·南漳模拟) 如图，已知菱形ABCD的边长为2，∠DAB=60°，则对角线BD的长是（）

A . 1 B . $\text{[math]}$ C . 2 D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·南漳模拟) 下列事件中，属于必然事件的是（）

A . 如果x²＝y² ，那么x＝y B . 车辆行驶到某十字路口，遇到绿灯 C . 掷一枚1元的硬币，有数字的面向上 D . 太阳每天都会从东方升起

答案解析收藏纠错 + 选题
9. (2021·南漳模拟) 如图，AB是⊙O的直径，⊙O的弦CD＝8，且CD⊥AB于点E. 若OE∶OB＝3∶5，则直径AB的长为（）

A . 16 B . 13 C . 10 D . 6

答案解析收藏纠错 + 选题
10. (2021·南漳模拟) 下列叙述正确的是（）

A . $\text{[math]}$ 的算术平方根是2 B . 函数y＝ $\text{[math]}$ 的自变量x的取值范围是x＞－1 C . 一元二次方程x²－2x＝4无实数根 D . 若点P（m，－1）与点Q（5，n）关于坐标原点对称，则m＝－5，n＝1

答案解析收藏纠错 + 选题

二、填空题

11. (2023九下·谷城模拟) 被命名为COVID-19新型冠状病毒的平均直径约是0.00 000 009米，将0.00 000 009用科学记数法表示为.

答案解析收藏纠错 + 选题
12. (2021·南漳模拟) 某校举行以“学党史，感党恩，听党话，跟党走”为主题的演讲比赛，决赛阶段只剩下甲、乙、丙、丁四名同学，则甲、乙同学获得前两名的概率是.

答案解析收藏纠错 + 选题
13. (2021·南漳模拟) 《九章算术》是中国古代一部数学专著，其中有一道阐述“盈不足术”的问题.原文：今有人共买物，人出八，盈三；人出七，不足四.问人数，物价各几何？译文：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元. 问共有多少人？这个物品的价格是元.

答案解析收藏纠错 + 选题
14. (2021·南漳模拟) 某种商品每件进价为20元，调查表明：在某段时间内，若以每件x元（20≤x≤40，且x为整数）出售，可卖出（40﹣x）件，若要使利润最大，则每件商品的售价应为元.

答案解析收藏纠错 + 选题
15. (2021·南漳模拟) 如图，△ABC内接于⊙O， E是边BC的中点，连接OE并延长交⊙O于点D，连接CD，若∠BCD＝26°，则∠A＝°.

答案解析收藏纠错 + 选题
16. (2021·南漳模拟) 如图，矩形ABCD中，AB＝5，BC＝3，E为边AB上一点，且BE＝3，△DAE沿DE翻折得到△DFE，连接BF，tan∠EFB的值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2024八下·武汉月考) 先化简，再求值： $\text{[math]}$ ，其中x＝ $\text{[math]}$ －2.

答案解析收藏纠错 + 选题
18. (2021·南漳模拟) 如图，△ABC中，AB＝AC，AD是边BC上的高.
1. （1）请用尺规作图法，作出线段AD的垂直平分线MN（保留作图痕迹，不必写出作法，但必须交待作图结果）；
2. （2）设（1）中的直线MN交边AB，AC分别于点E，F ，连接DE，DF.求证：四边形AEDF是菱形.
答案解析收藏纠错 + 选题
19. (2021·南漳模拟) 为了解学生掌握垃圾分类知识的情况，某校举行有关垃圾分类的知识测试活动，现从七、八年级中各随机抽取20名学生的测试成绩（满分10分，6分及6分以上为合格）进行整理、描述和分析，下面给出了部分信息.
七年级20名学生的测试成绩为：

7，8，7，9，7，6，5，9，10，9，8，5，8，7，6，7，9，7，10，6.

八年级20名学生的测试成绩条形统计图如图所示：

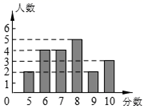
七，八年级抽取的学生的测试成绩的平均数、众数、中位数如表所示：

年级

平均数

众数

中位数

七年级

7.5

b

7

八年级

a

8

c

请你根据以上提供信息，解答下列问题：
1. （1）上表中a＝，b＝，c＝；
2. （2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好？请说明理由（写出一条理由即可）；
3. （3）该校七、八年级共1100名学生参加了此次测试活动，估计参加此次测试活动成绩合格的学生有人.
答案解析收藏纠错 + 选题
20. (2021·南漳模拟) 如图，某中学数学兴趣小组在学习了“解直角三角形及其应用”后，选定测量小河对岸一幢建筑物BC的高度，他们先在A处测得该建筑物顶端B的仰角为28°，然后从A处前进40m到达D处，在D处测得该建筑物顶端B的仰角为60°，点A，D， C在同一水平的直线上，且BC⊥DC. 求建筑物BC的高度（结果精确到0.1）.
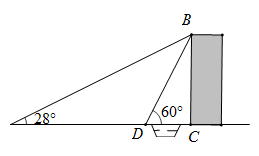
（参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53， $\text{[math]}$ ≈1.73）

答案解析收藏纠错 + 选题

21. (2021·南漳模拟) 张明丽同学学习了反比例函数 y＝－ $\text{[math]}$ 的图象和性质后，对新函数y＝－ $\text{[math]}$ 的图象和性质进行了探究，以下是她的探究过程：

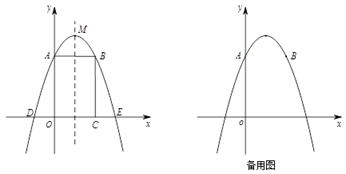
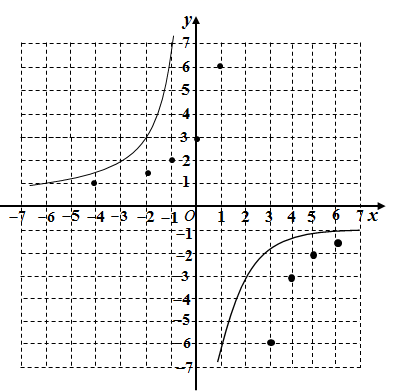
第一步：在平面直角坐标系中，作出函数 y＝－ $\text{[math]}$ 的图象；

第二步：通过列表、描点、连线，作出新函数y＝－ $\text{[math]}$ 的图象；

①列表：

x	…	－4	－2	－1	0	1	3	4	5	6	…
y	…	1	$\text{[math]}$	2	3	6	－6	－3	－2	－ $\text{[math]}$	…

②描点：如图所示

（1）请在图中帮助张明丽同学完成连线步骤；
（2）观察函数图象，发现函数y＝－ $\text{[math]}$ 与函数 y＝－ $\text{[math]}$ 的图象都是双曲线，并且形状也相同，只是位置发生了改变，由此可知，函数y＝－ $\text{[math]}$ 的图象可由函数 y＝－ $\text{[math]}$ 的图象平移得到.请结合图象写出函数y＝－ $\text{[math]}$ 的两条性质（函数的增减性和对称性各一条）.

答案解析收藏纠错 + 选题

22. (2021·南漳模拟) 如图，在等腰△ABC中，AB＝BC，以AB为直径的⊙O与AC相交于点D，与CB的延长线相交于点E，过点D作DF⊥BC交AB的延长于点F，垂足为点M.
1. （1）判定直线DF与⊙O的位置关系，并说明理由；
2. （2）若BF＝4，∠F＝30°，求图中阴影部分的面积.
答案解析收藏纠错 + 选题
23. (2021·南漳模拟) 某校计划对100名获优秀作品一、二、三等奖的学生分别奖励一套数学用具、一本笔记本、一支水笔. 已知购买1套数学用具和2本笔记本共35元，购买2套数学用具和3本笔记本共60元，一支水笔的单价为2元. 已知获一等奖人数最少，获三等奖的人数最多.
1. （1）求数学用具和笔记本的单价；
2. （2）因购买数量较多，商家给予优惠：每买1套数学用具和1本笔记本赠送2支水笔；
  ①若获二等奖人数是获一等奖人数的1.5倍，且获一等奖人数超过20人，已知在购买奖品时仍需要购买水笔，求购买奖品的总金额；
  
  ②若赠送的水笔恰好奖励给获三等奖的学生，求购买奖品的总金额的最小值及获二等奖的人数.
答案解析收藏纠错 + 选题
24. (2021·南漳模拟) 在△ABC中，AB＝AC，∠BAC＝α，点P是△ABC外一点，连接BP，将线段BP绕点P逆时针旋转α得到线段PD，连接BD，CD，AP.
观察猜想：
1. （1）如图1，当α＝60°时， $\text{[math]}$ 的值为，直线CD与 AP所成的较小角的度数为°；
  类比探究：
2. （2）如图2，当α＝90°时，求出 $\text{[math]}$ 的值及直线CD与AP所成的较小角的度数；
3. （3）如图3，当α＝90°时，点E，F分别为AB，AC的中点，点P在线段FE的延长线上，点A，D，P三点在一条直线上，BD交PF于点G，CD交AB于点H. 若CD＝2＋ $\text{[math]}$ ，求BD的长.
答案解析收藏纠错 + 选题
25. (2021·南漳模拟) 在平面直角坐标系xOy中，矩形OABC的顶点A，C的坐标分别为（0，3），（2，0），顶点为M的抛物线y＝－x²＋bx＋c经过点A，B，且与x轴交于点D，E（点D在点E的左侧）.
1. （1）直接写出点B的坐标，抛物线的解析式及顶点M的坐标；
2. （2）点P是（1）中抛物线对称轴上一动点，求△PAD的周长最小时点P的坐标；
3. （3）平移抛物线y＝－x²＋bx＋c，使抛物线的顶点始终在直线AM上移动，在平移的过程中，当抛物线与线段BM有公共点时，求抛物线顶点的横坐标a的取值范围.
答案解析收藏纠错 + 选题