四川省成都市天府新区2020-2021学年八年级下学期数学期...

更新时间：2021-08-23 浏览次数：215 类型：期末考试

一、单选题

1. (2021八下·成都期末) 已知m＜n，下列不等式一定成立的是（）

A . 3m＜3n B . m﹣6＞n﹣6 C . ﹣2m＜﹣2n D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·铜梁期末) 下面图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022八下·清城期中) 将点A（2，﹣1）向左平移4个单位长度得到点B，则点B的坐标是（）

A . （﹣2，﹣1） B . （6，﹣1） C . （2，3） D . （2，﹣5）

答案解析收藏纠错 + 选题
4. 下列因式分解正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021八下·成都期末) 如图，△DEF是由△ABC沿射线AB方向经过平移得到的，若∠A＝33°，则∠EDF的度数为（）

A . 33° B . 80° C . 57° D . 67°

答案解析收藏纠错 + 选题
6. (2021八下·成都期末) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2021八下·成都期末) 若x＝﹣1是关于x的分式方程 $\text{[math]}$ 的解，则a的值为（）

A . ﹣1 B . 1 C . ﹣ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021八下·成都期末) 下列命题正确的是（）

A . 一组对边平行，另一组对边相等的四边形是平行四边形； B . 对角线互相垂直的四边形是菱形； C . 对角线相等的四边形是矩形； D . 一组邻边相等的矩形是正方形

答案解析收藏纠错 + 选题
9. (2021八下·成都期末) 函数y=kx+b（k、b为常数，k≠0）的图象如图，则关于x的不等式kx+b＞0的解集为（）

A . x＞0 B . x＜0 C . x＜2 D . x＞2

答案解析收藏纠错 + 选题
10. (2023九上·成都开学考) 如图，在平行四边形ABCD中，∠ABC的平分线交AD于点E，过点A作AF⊥BE，垂足为点F，若AF＝5，BE＝24，则CD的长为（）

A . 8 B . 13 C . 16 D . 18

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·云岩模拟) 若分式 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
12. (2024九上·重庆市月考) 一个多边形的内角和是720°，这个多边形的边数是．

答案解析收藏纠错 + 选题
13. (2021八下·成都期末) 如图，在△ABC中，D，E分别是边AB，AC的中点，BC=10，则DE的长为.

答案解析收藏纠错 + 选题
14. (2021八下·成都期末) 如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于 $\text{[math]}$ BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连结CD．若CD＝AC，∠A＝48°，则∠ACB＝．

答案解析收藏纠错 + 选题
15. (2021八下·成都期末) 已知a²﹣b²＝18，a﹣b＝3，则代数式a+b﹣2的值为.

答案解析收藏纠错 + 选题
16. (2021八下·成都期末) 关于x的一次函数y＝（a+1）x+a的图象经过第一、三、四象限，则a的取值范围是.

答案解析收藏纠错 + 选题
17. (2021八下·成都期末) 若从﹣1，0，1，2，3这五个数中任抽取一个数作为a的值，使关于x的方程 $\text{[math]}$ ＝1的解大于1，则抽到符合条件的a值的概率是.

答案解析收藏纠错 + 选题
18. (2021八下·成都期末) 如图，在平面直角坐标系中，直线y＝﹣x+2与x轴交于点A，与y轴交于点B，点P是线段AB的三等分点（AP＞BP），点C是x轴上的一个动点，连接BC，以BC为直角边，点B为直角顶点作等腰直角△BCD，连接DP.则DP长度的最小值是.

答案解析收藏纠错 + 选题
19. (2021八下·成都期末) 如图，正方形ABCD边长为 $\text{[math]}$ ，△BCD绕B顺时针旋转至△BFE，点C与点F对应，点D与点E对应，连接AE，交BD于点P，当P是AE的中点时，△AEB的面积为.

答案解析收藏纠错 + 选题

三、解答题

20. (2021八下·成都期末)
1. （1）分解因式：3x³﹣12x.
2. （2）解不等式组： $\text{[math]}$ ，并写出它的整数解.
答案解析收藏纠错 + 选题
21. (2024八下·南宁月考) 先化简，再求值： $\text{[math]}$ ，其中x＝ $\text{[math]}$ .

答案解析收藏纠错 + 选题
22. (2021八下·成都期末) 如图，在平面直角坐标系中，已知点A（﹣5，2），B（﹣4，5），C（﹣3，3）.

（ 1 ）画出△ABC.

（ 2 ）画出△A₁B₁C₁ ，使△A₁B₁C₁与△ABC关于原点O成中心对称；

（ 3 ）将△ABC先向右平移6个单位长度，再向下平移1个单位长度，得到△A₂B₂C₂ ，请画出平移后的△A₂B₂C₂.

答案解析收藏纠错 + 选题
23. (2021九上·茂南月考) 如图，在平行四边形ABCD中，点M，N分别在AB，CD上，AC与MN交于点O，且AO＝CO，连接AN，CM.
1. （1）求证：AM＝CN；
2. （2）已知：AC＝8，MN＝6，且MN⊥AC，求四边形AMCN的周长.
答案解析收藏纠错 + 选题
24. (2021八下·成都期末) 生活垃圾处理是关系民生的基础性公益事业，加强生活垃圾分类处理，维护公共环境和节约资源是全社会共同的责任，已知某小区购进A型和B型两种分类垃圾桶，购买A型垃圾桶花费了1000元，购买B型垃圾桶花费了750元，已知购买一个A型垃圾桶比购买一个B型垃圾桶少花10元，且购买的A型垃圾桶的数量是购买的B型垃圾桶的数量的2倍.
1. （1）求购买一个A型垃圾桶和一个B型垃圾桶各需多少元？
2. （2）根据上级部门的要求，小区还需要增加购买A型和B型垃圾桶共30个，若总费用不超过700元，求增加购买A型垃圾桶的数量至少是多少个？
答案解析收藏纠错 + 选题
25. (2021八下·成都期末) 在Rt△ABC中，∠BAC＝90°，设∠ACB＝60°，将△ABC绕着点C顺时针旋转，得到△CDE（点D，E分别与B，A对应），连接BD.
1. （1）如图1，当点D在线段CA的延长线上时，若AD＝5，求BD的长；
2. （2）如图2，当点D在如图所示位置时，连接EA并延长交BD于F，过点D作DG∥AB交线段EA的延长线于G，连接AD，BG.求证：四边形ADGB为平行四边形.
3. （3）在（2）的条件下，如图3，连接CF，若AC＝5，CF＝8，求EF的长.
答案解析收藏纠错 + 选题
26. (2021八下·成都期末) 2020年8月底，天府新区根据鹿溪河全流域水环境治理工程建设总体安排，启动了兴隆湖水生态综合提升工程，其中一项工程计划工期10个月，工程总长度为10千米，由甲、乙两个工程队负责施工已知甲工程队每月改造1.2千米，乙工程队每月改造0.8千米，已知甲工程队每千米的施工费用为80万元，乙工程队每千米的施工费用为60万元，设完成此项工程所需施工总费用为w万元，甲工程队完成的工程长度为x千米.
1. （1）写出w与x的函数表达式；
2. （2）由于受场地施工限制，甲、乙两工程队不能同时施工，在保证不超过计划工期内完成此项工程的情况下，甲工程队需改造多少千米才能使两工程队完成此项工程所需施工总费用最低？最低费用为多少？
答案解析收藏纠错 + 选题
27. (2021八下·成都期末) 如图1，在矩形ABCD中，AM平分∠BAD，交BC于点M，点N是AD上的一点，连接MN，MD，且MN＝MD，过点D作DF⊥MN于F，DF延长线交AM于E，过点E作EP⊥AD于P.
1. （1）如图1，①若CD＝5，AD＝7，求线段CM的长；
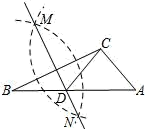
  ②求证：△PED≌△CMD.
2. （2）如图2，过点F作FH⊥CD于H，当AM＝AD时，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
28. (2021八下·成都期末) 在平面直角坐标系中，点A坐标为（0，4），点B坐标为（﹣3，0），连接AB，过点A作AC⊥AB交x轴于点C，点E是线段AO上的一动点.
1. （1）如图1，当AE＝3OE时，
  ①求直线BE的函数表达式；
  
  ②设直线BE与直线AC交于点D，连接OD，点P是直线AC上的一动点（不与A，C，D重合），当S_△BOD＝S_△PDB时，求点P的坐标；
2. （2）如图2，设直线BE与直线AC的交点F，在平面内是否存在点M使以点A，E，F，M为顶点的四边形是菱形？若存在，请直接写出点M的坐标；若不存在，请简述理由.
答案解析收藏纠错 + 选题