吉林省长春市宽城区2020-2021学年八年级下学期数学期末...

更新时间：2021-09-23 浏览次数：171 类型：期末考试

一、单选题

1. (2021八下·宽城期末) 要使根式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . x＞1 B . x≥1 C . x＜1 D . x≤1

答案解析收藏纠错 + 选题
2. (2021八上·长春期中) 在平面直角坐标系中，点P（3，-4）到x轴的距离是（）

A . 3 B . -3 C . 4 D . -4

答案解析收藏纠错 + 选题
3. (2020九上·任城期中) 下列各点中，在反比例函数 $\text{[math]}$ 图象上的是

A . （－1，8） B . （－2，4） C . （1，7） D . （2，4）

答案解析收藏纠错 + 选题
4. (2024九下·叙州月考) 某校评选先进班集体，从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分，各项满分均为 $\text{[math]}$ ，所占比例如下表：

项目

学习

卫生

纪律

活动参与

所占比例

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

八年级 $\text{[math]}$ 班这四项得分依次为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则该班四项综合得分（满分 $\text{[math]}$ ）为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·南岗期中) 如图，在△ABC中，∠A＝40°，AB＝AC，点D在AC边上，以CB，CD为边作▱BCDE，则∠E的度数为（）

A . 40° B . 50° C . 60° D . 70°

答案解析收藏纠错 + 选题
6. (2022·绍兴模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的中线，四边形 $\text{[math]}$ 是平行四边形，增加下列条件，能判断 $\text{[math]}$ 是菱形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021八下·宽城期末) 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖的面积为a，小正方形地砖的面积为b，依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD的面积为（）

A . a+b B . a-b C . 2a+b D . 2a-b

答案解析收藏纠错 + 选题
8. (2021八下·宽城期末) 如图，矩形 $\text{[math]}$ 的顶点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 和点 $\text{[math]}$ 在 $\text{[math]}$ 边上， $\text{[math]}$ ，连接 $\text{[math]}$ 轴，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . 3 C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·宽城期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2023九下·南浔模拟) 若一次函数 $\text{[math]}$ 的图像与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
11. (2021八下·宽城期末) 如图，在平行四边形ABCD中，点E是CD的中点，AE、BC的延长线交于点F．若△ECF的面积为1，则平行四边形ABCD的面积为．

答案解析收藏纠错 + 选题
12. (2020八上·普宁期中) 如图，在平面直角坐标系中，点P是正比例函数y＝x图象上的一点，点A的坐标为（0，1），点B的坐标为（4，1），当PB+PA取最小值时，点P的坐标为．

答案解析收藏纠错 + 选题
13. (2021八下·宽城期末) 如图， $\text{[math]}$ ， $\text{[math]}$ 是正方形 $\text{[math]}$ 的对角线 $\text{[math]}$ 上的两点， $\text{[math]}$ ， $\text{[math]}$ ，则四边形 $\text{[math]}$ 的周长是．

答案解析收藏纠错 + 选题
14. (2021·巴州模拟) 点P，Q，R在反比例函数 $\text{[math]}$ （常数k＞0，x＞0）图象上的位置如图所示，分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S₁ ， S₂ ， S₃.若OE＝ED＝DC，S₁＋S₃＝27，则S₂的值为.

答案解析收藏纠错 + 选题

三、解答题

15. (2021八下·宽城期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022八下·赞皇期中) 如图，点E，F在 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．求证：四边形 $\text{[math]}$ 是平行四边形．

答案解析收藏纠错 + 选题
17. (2021八下·宽城期末) 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图象与函数 $\text{[math]}$ （m >0，x>0）的图象交于A（3，a）、B（14-2a，2）两点．
1. （1）求m的值．
2. （2）求一次函数 $\text{[math]}$ 所对应的函数表达式．
答案解析收藏纠错 + 选题
18. (2022八下·婺城期末) 图①、图②、图③均是5×5的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A、B均在格点上．只用无刻度的直尺，在给定的网格中按下列要求画图，所画图形的顶点均在格点上且不全等，不要求写画法．
1. （1）在图①中以线段AB为边画一个平行四边形．
2. （2）在图②中以线段AB为边画一个正方形．
3. （3）在图③中以线段AB为边画一个菱形，所画菱形的面积为．
答案解析收藏纠错 + 选题
19. (2023八下·开州期末) 如图，在△ABC中，AB＝AC ，点D、E分别是线段BC、AD的中点，过点A作BC的平行线交BE的延长线于点F ，连接CF ．
1. （1）求证：△BDE≌△FAE；
2. （2）求证：四边形ADCF为矩形．
答案解析收藏纠错 + 选题

20. (2021八下·宽城期末) 某校拟派一名跳高运动员参加校际比赛，对甲、乙两名同学进行了8次跳高选拔比赛，他们的原始成绩（单位：cm）如下表：

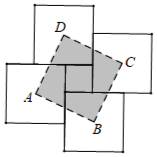
次数

成绩

学生

第1次

第2次

第3次

第4次

第5次

第6次

第7次

第8次

甲

169

165

168

169

172

173

169

167

乙

161

174

172

162

163

172

176

两名同学的8次跳高成绩数据分析如下表：

名称

成绩

学生

平均数

（单位：cm）

中位数

（单位：cm）

众数

（单位：cm）

方差

（单位：cm²）

甲

5.75

乙

169

172

31.25

根据图表信息回答下列问题：

（1）求a、b、c的值．
（2）这两名同学中，的成绩更为稳定（填“甲”或“乙”）．
（3）若预测跳高165cm就可能获得冠军，该校为了获取跳高比赛冠军，你认为应该选择哪位同学参赛，并说明理由

答案解析收藏纠错 + 选题

21. (2021八下·宽城期末) 如图，在四边形ABCD中，AD $\text{[math]}$ BC，AB= AD，∠BAD的平分线交BC于点E，连结DE．
1. （1）求证：四边形ABED是菱形．
2. （2）连结BD．若CE=2BE，AE=4，BD=6，则△CDE的面积是．
答案解析收藏纠错 + 选题
22. (2021八下·宽城期末) 已知A、B两地之间有一条公路．甲车从A地出发匀速开往B地，甲车出发2小时后，乙车从B地出发匀速开往A地，甲车出发6小时，两车同时到达各自的目的地．两车行驶的路程之和y（千米）与甲车行驶的时间x（时）之间的函数关系如图所示．
1. （1）甲车的速度为千米/时，a的值为．
2. （2）求乙车出发后，y与x之间的函数关系式．
3. （3）当甲、乙两车相距100千米时，求甲车行驶的时间．
答案解析收藏纠错 + 选题
23. (2021八下·宽城期末) （教材呈现）下图是华师版八年级下册数学教材第121页的部分内容．
1. （1）（问题解决）如图①，已知矩形纸片 $\text{[math]}$ ，将矩形纸片沿过点 $\text{[math]}$ 的直线折叠，使点 $\text{[math]}$ 落在边 $\text{[math]}$ 上，点 $\text{[math]}$ 的对应点为 $\text{[math]}$ ，折痕为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上．求证：四边形 $\text{[math]}$ 是正方形．
2. （2）（规律探索）由（问题解决）可知，图①中的 $\text{[math]}$ 为等腰三角形．现将图①中的点 $\text{[math]}$ 沿 $\text{[math]}$ 向右平移至点 $\text{[math]}$ 处（点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），如图②，折痕为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 上，那么 $\text{[math]}$ 还是等腰三角形吗？请说明理由．
3. （3）（结论应用）在图②中，当 $\text{[math]}$ 时，将矩形纸片继续折叠如图③，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，折痕为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上．要使四边形 $\text{[math]}$ 为菱形，则 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2021八下·宽城期末)
1. （1）模型建立：如图①，在Rt△ABC中，∠ACB=90°，AC=BC．直线ED经过点C，过点A作AD⊥ED于D，过点B作BE⊥ED于E．求证：△BEC≌△CDA．
2. （2）模型应用：
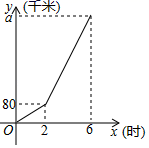
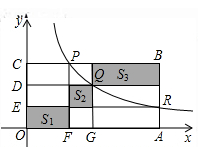
  如图②，在平面直角坐标系中，直线l₁： $\text{[math]}$ 交x轴于点A，交y轴于点B，将直线l₁绕着点B逆时针旋转45°至l₂ ．过点A作AC⊥l₁交l₂于点C，过点C作CD⊥x轴于点D．求直线l₂所对应的函数表达式．
3. （3）如图③，在矩形ABCO中，O为坐标原点，点B的坐标为（8，-6），A、C两点分别在x轴、y轴上．P是线段AB上的动点，点D在第四象限，且是直线y=-2x+6上的一点．若△PCD是不以点C为直角顶点的等腰直角三角形，直接写出点D的横坐标．
答案解析收藏纠错 + 选题