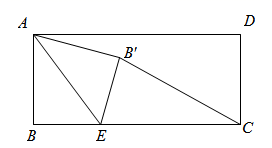
B .
B .  C .
C .  D .
D . 
| 选手 | | | | | | 平均成绩 | 中位数 |
| 成绩/分 | 86 | ■ | 82 | 88 | 82 | 85 | ■ |
则上表中被遮盖的两个数据从左到右依次是( )


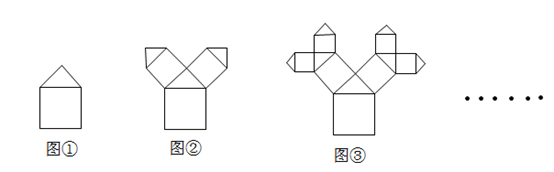
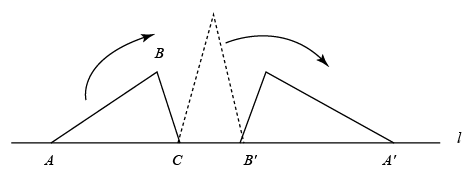
收集数据:142 149 150 153 156 159 160 165 165 165 166 168 168 169 170 174 176 178 178 178 180 182 188 189 197
整理数据:通过计算可知样本平均数为 .
频数分布统计表
| 分组 | | | | | | |
| 频数 | 1 | 4 | 8 | | | 2 |
根据以上信息回答下列问题:
②女生立定跳远成绩达到 及以上成绩时为优秀,则样本的优秀率为.
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
7 |
6 |
5 |
4 |
|
2 |
|
0 |
|
|
7 |
5.2 |
4.6 |
5.0 |
5.6 |
6.2 |
6.7 |
7 |