 B .
B .  C .
C .  D .
D . 



学生身高的频数分布表
| 组别 | 身高(单位: | 频数 |
| | | 15 |
| | | |
| | | 35 |
| | | 15 |
| | | 5 |

请结合图表中提供的信息,解答下列问题:
①当 度时,四边形
为菱形;
②当 时,四边形
为正方形.
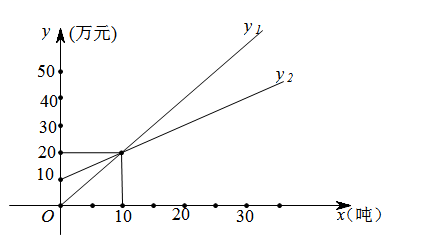
① 的解析式为;
的解析式为.
②当销售量( )满足条件时,该公司盈利(即收入大于成本).

| 课题 | 测量旗杆的高度 | |
| 测量工具 | 测量角度(单位:度)的仪器、测量距离(单位: | |
| 测量成员 | 小明 | 小东 |
| 测量方案 示意图 | | |
| 示意图说明 | 如图,旗杆的最高点 | |
| 测量数据 | | |
| 参考数据 | | |

如图1,在矩形 中,
,
,圆弧
过点
和
延长线上的点
,圆心
在
上,
上有一个动点
,
,交直线
于点
.线段
的长
与
的长
以及
的长
之间的几组对应值如下表所示.
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| | 0 | 1 | 2 | 2.9 | 3.9 | 4.7 | 5.3 | 5.5 | 4.8 |
| | 4.3 | 4.4 | 4.3 | 4.1 | 3.5 | 2.7 | 1.7 | 1.2 | 2.6 |
线段 的长度的最大值约为;
线段 的长度的最小值约为;
圆弧 所在圆的半径约等于;
连结 ,
面积的最大值约为.