
 B .
B . 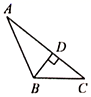 C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 



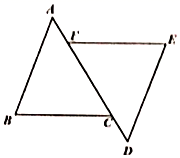

求:⑴∠EBC的度数;
⑵∠A的度数.对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
解:⑴∵CD⊥AB(已知),
∴∠CDB= ▲ .
∵∠EBC=∠CDB+∠BCD( ).
∴∠EBC= ▲ +35°= ▲ (等量代换).
⑵∵∠EBC=∠A+∠ACB( ),
∴∠A=∠EBC﹣∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A= ▲ ﹣90°= ▲ (等量代换).

|
如图,已知△ABC分别用∠1、∠2、∠3表示△ABC的三个内角,证明∠1+∠2+∠3=180°. 解:延长BC至点E,以点C为顶点,在BE的上侧作∠DCE=∠2,则CD∥BA(同位角相等,两直线平行) |

①如图二,在△ABC中,∠A=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.
②如图三,将△ABC的∠A折叠,使点A落在△ABC外的A1处,折痕为DE.若∠A=α,∠BDA1=β,∠CEA1=γ,则α、β、γ满足的等量关系为 ▲ (用含α、β、γ的代数式表示).
