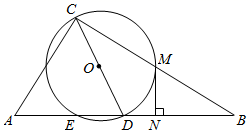
 B .
B .  C .
C .  D .
D . 


甲分厂产品等级的频数分布表
|
等级 |
A |
B |
C |
D |
|
频数 |
40 |
20 |
20 |
20 |
乙分厂产品等级的频数分布表
|
等级 |
A |
B |
C |
D |
|
频数 |
28 |
17 |
34 |
21 |