河南省洛阳市洛龙区2020-2021学年九年级上学期数学期中...

更新时间：2021-10-28 浏览次数：151 类型：期中考试

一、单选题

1. (2020九上·孟村期末) 点 $\text{[math]}$ 关于原点对称的点为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·鼓楼月考) 按照我国《生活垃圾管理条例》要求，到 $\text{[math]}$ 年底，我国地级及以上城市要基本建成垃圾分类处理系统，下列垃圾分类指引标志图形中，是轴对称图形又是中心对称图形的是（）

A . 厨余垃圾 $\text{[math]}$ B . 可回收物 $\text{[math]}$ C . 有害垃圾 $\text{[math]}$ D . 其他垃圾 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·顺德月考) 若关于x的方程kx²﹣x＋3＝0有实数根，则k的取值范围是（）

A . k≤12 B . k≤ $\text{[math]}$ C . k≤12且k≠0 D . k≤ $\text{[math]}$ 且k≠0

答案解析收藏纠错 + 选题
4. (2021九上·呼和浩特期中) 函数y＝ax²﹣a与y＝ax﹣a（a≠0）在同一坐标系中的图象可能是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2020九上·洛龙期中) 如图，已知 $\text{[math]}$ 和 $\text{[math]}$ 关于点 $\text{[math]}$ 成中心对称，则下列结论错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·鄞州期中) 已知二次函数 $\text{[math]}$ ，则下列关于这个函数图象和性质的说法，正确的是（）

A . 图象的开口向上 B . 图象的顶点坐标是 $\text{[math]}$ C . 当 $\text{[math]}$ 时，y随x的增大而增大 D . 图象与x轴有唯一交点

答案解析收藏纠错 + 选题
7. (2020九上·洛龙期中) 如图，已知点 $\text{[math]}$ ， $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转到 $\text{[math]}$ ，点 $\text{[math]}$ 与 $\text{[math]}$ 是对应点，则点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八下·杭州期中) 若关于x的一元二次方程ax²＋bx＋2＝0（a≠0）有一根为x＝2019，则一元二次方程a（x﹣1）²＋b（x﹣1）＝﹣2必有一根为（）

A . 2017 B . 2020 C . 2019 D . 2018

答案解析收藏纠错 + 选题
9. (2020九上·洛龙期中) 将 $\text{[math]}$ 绕点B按逆时针方向旋转 $\text{[math]}$ 到 $\text{[math]}$ 的位置，斜边 $\text{[math]}$ 和 $\text{[math]}$ 相交于点F，则 $\text{[math]}$ 的度数等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九上·洛龙期中) 已知二次函数y＝ax²+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x＝1，其图象的一部分如图所示，下列说法中：①abc＜0；②2a+b＝0；③当﹣1＜x＜3时，y＞0；④a﹣b+c＜0；⑤2c﹣3b＞0．其中正确结论的个数是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·洛龙期中) 若方程 $\text{[math]}$ 的一个根为 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2021八下·沂源期中) 一人患了流感，经过两轮传染后共有64人患了流感.如果不及时控制，第三轮将又有人被传染.

答案解析收藏纠错 + 选题

13. (2020九上·洛龙期中) 已知二次函数 $\text{[math]}$ 自变量x的部分取值和对应函数值y如表：

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

则在实数范围内能使得 $\text{[math]}$ 成立的x取值范围是.

答案解析收藏纠错 + 选题

14. (2020九上·洛龙期中) 如图， $\text{[math]}$ ， $\text{[math]}$ ，线段 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ 至 $\text{[math]}$ ，则C点的坐标为.

答案解析收藏纠错 + 选题
15. (2020九上·洛龙期中) 如图，抛物线 $\text{[math]}$ 与x轴交于点A、B，把抛物线在x轴及其上方的部分记作 $\text{[math]}$ ，将 $\text{[math]}$ 向右平移得 $\text{[math]}$ ， $\text{[math]}$ 与x轴交于点B， $\text{[math]}$ 若直线 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 共有3个不同的交点，则m的取值范围是

答案解析收藏纠错 + 选题

三、解答题

16. (2020九上·洛龙期中) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
17. (2020九上·洛龙期中) 如图，在直角坐标系中，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点， $\text{[math]}$ 和 $\text{[math]}$ 的顶点都在格点上，已知A点坐标为（-3，-2）结合所给的平面直角坐标系解答下列问题：

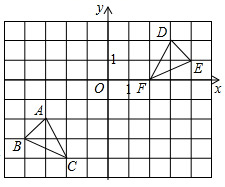
（ 1 ）画出△ABC向上平移4个单位长度后所得到的 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的坐标；

（ 2 ）画出 $\text{[math]}$ 绕点O按顺时针方向旋转 $\text{[math]}$ 后所得到的 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的坐标；

（ 3 ）判断 $\text{[math]}$ 和 $\text{[math]}$ 是否是关于某点成为中心对称的图形，若是，请直接写出对称中心的坐标；若不是，请说明理由.

答案解析收藏纠错 + 选题
18. (2020九上·洛龙期中) 阅读材料：
如果 $\text{[math]}$ ， $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的两根，那么有： $\text{[math]}$ ， $\text{[math]}$ .这是一元二次方程根与系数的关系，我们利用它可以用来解题.

例： $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两根，求 $\text{[math]}$ 的值.

解 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两根

$\text{[math]}$ ， $\text{[math]}$

$\text{[math]}$ .

请你根据以上解法解答下题：
1. （1）已知：关于x的一元二次方程 $\text{[math]}$ .
  ①求证：无论m取什么实数值，方程总有两个不相等的实数根；
  
  ②若 $\text{[math]}$ ， $\text{[math]}$ 是原方程的两个实数根，且满足 $\text{[math]}$ ，求m的值.
2. （2）设m、n是方程 $\text{[math]}$ 的两个实数根，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
19. (2021·河南模拟) 在平面直角坐标系xOy中，直线y=﹣ $\text{[math]}$ x+5与x轴、y轴分别交于点A、B(如图)．抛物线y=ax²+bx(a≠0)经过点A ．
1. （1）求线段AB的长；
2. （2）如果抛物线y=ax²+bx经过线段AB上的另一点C ，且BC= $\text{[math]}$ ，求这条抛物线的表达式；
3. （3）如果抛物线y=ax²+bx的顶点D位于△AOB内，求a的取值范围．
答案解析收藏纠错 + 选题
20. (2020九上·洛龙期中) 某车间生产以甲、乙两种水果为原料的某种罐头，在一次进货中得知，花费 $\text{[math]}$ 万元购进的甲种水果与 $\text{[math]}$ 万元购进的乙种水果质量相同，乙种水果每千克比甲种水果多 $\text{[math]}$ 元.
1. （1）求甲、乙两种水果的单价；
2. （2）车间将水果制成罐头投入市场进行售卖，已知一听罐头需要甲乙水果各 $\text{[math]}$ 千克，而每听罐头的成本除了水果成本之外，其他所有成本是水果成本的 $\text{[math]}$ 还要多 $\text{[math]}$ 元.调查发现，以 $\text{[math]}$ 元的定价进行销售，每天只能卖出 $\text{[math]}$ 听，超市对它进行促销，每降低 $\text{[math]}$ 元，平均每天可多卖出 $\text{[math]}$ 听，当售价为多少元时，利润最大？最大利润为多少？
3. （3）若想使得该种罐头的销售利润每天达到 $\text{[math]}$ 万元，并且保证降价的幅度不超过定价的 $\text{[math]}$ ，每听罐头的价钱应为多少钱？
答案解析收藏纠错 + 选题
21. (2020九上·洛龙期中) 如图，已知抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 和点 $\text{[math]}$ ，与y轴交于点C.
1. （1）求此抛物线的解析式；
2. （2）若点P是直线 $\text{[math]}$ 下方的抛物线上一动点（不点B，C重合），过点P作y轴的平行线交直线 $\text{[math]}$ 于点D，设点P的横坐标为m.
  ①用含m的代数式表示线段 $\text{[math]}$ 的长.
  
  ②连接 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积最大时点P的坐标.
答案解析收藏纠错 + 选题

22. (2020九上·洛龙期中) 小云在学习过程中遇到一个函数 $\text{[math]}$ .下面是小云对其探究的过程，请补充完整：

（1）当 $\text{[math]}$ 时，对于函数 $\text{[math]}$ ，即 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 随x的增大而，且 $\text{[math]}$ ；对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 随x的增大而，且 $\text{[math]}$ ；结合上述分析，进一步探究发现，对于函数y，当 $\text{[math]}$ 时，y随x的增大而.

（2）当 $\text{[math]}$ 时，对于函数y，当 $\text{[math]}$ 时，y与x的几组对应值如下表：

$\text{[math]}$	0	$\text{[math]}$	1	$\text{[math]}$	2	$\text{[math]}$	3	$\text{[math]}$
$\text{[math]}$	0	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

综合上表，进一步探究发现，当 $\text{[math]}$ 时，y随x的增大而增大.在平面直角坐标系 $\text{[math]}$ 中，画出当 $\text{[math]}$ 时的函数y的图象.

（3）过点(0，m)（ $\text{[math]}$ ）作平行于x轴的直线l，结合（1）（2）的分析，解决问题：若直线l与函数 $\text{[math]}$ 的图象有两个交点，则m的最大值是.

答案解析收藏纠错 + 选题

23. (2020九上·洛龙期中) 如图①，正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点B、C分别在边 $\text{[math]}$ 、 $\text{[math]}$ 上，且 $\text{[math]}$ ，此时显然 $\text{[math]}$ ， $\text{[math]}$ 成立.
1. （1）如图②，当 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 时，那么 $\text{[math]}$ 和 $\text{[math]}$ 还成立吗？若成立，请证明；若不成立，请说明理由；
2. （2）如图③ $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点H；当 $\text{[math]}$ ， $\text{[math]}$ 时，则线段 $\text{[math]}$ 的长为.
答案解析收藏纠错 + 选题