19.
(2021九上·六安月考)
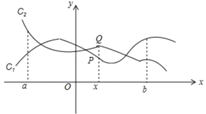
如图,点P(x,y
1)与Q(x,y
2)分别是两个函数图象C
1与C
2上的任一点,当a≤x≤b时,有-1≤y
1-y
2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y
1)与Q(x,y
2)分别是两个函数y=3x+1与y=2x-1图像上的任一点,当-3≤x≤-1时,y
1-y
2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2,并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y
1-y
2≤1成立,因此这两个函数在-3≤x≤-1是“相邻函数”.


 B .
B . 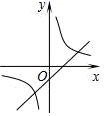 C .
C . 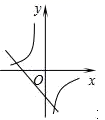 D .
D . 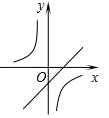

 B .
B . 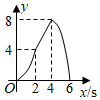 C .
C .  D .
D .