
 B .
B .  C .
C .  D .
D . 

| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 收入(点) | 15 | 21 | 27 | 27 | 21 | 30 | 21 |

①∠AED+∠EAC+∠EDB=90°,②AP=FP,③AE= AO,④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36,⑤CE•EF=EQ•DE.其中正确的结论有( )



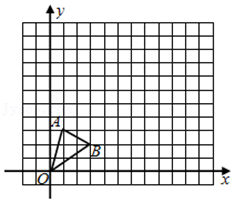
△O″A″B;


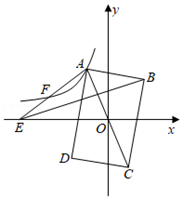

求证:△BOP∽△PCE;