

 B .
B .  C .
C .  D .
D . 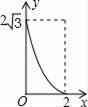
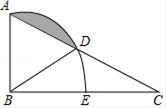

①4ac<b2;② ;③
;④当y<0时,x的取值范围是-1<x<3;⑤当x<0时,y随x增大而增大;⑥方程ax2+bx+c=2有两个不等的实数根,其中结论正确的结论的序号是.
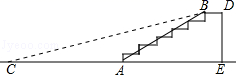
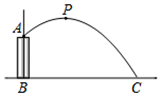
其中正确的是(写出所有正确结论的序号).
|
类别 |
分数段 |
频数(人数) |
|
A |
| a |
| B | | 16 |
| C | | 24 |
| D | | 6 |