浙江省杭州市萧山区高桥初中教育集团2021-2022学年九年...

更新时间：2024-07-31 浏览次数：109 类型：月考试卷

一、仔细选一选（本题有10个小题，共30分）下面每小题给出的四个选项中，只有一个是正确的.

1. (2021九上·萧山月考) 抛物线y＝3x²﹣2的顶点坐标是（　　）

A . （0，﹣2） B . （﹣2，0） C . （2，0） D . （0，0）

答案解析收藏纠错 + 选题
2. (2021九上·萧山月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·萧山月考) 下列说法正确的是（　　）

A . 同时投掷两枚相同的硬币，出现“一正一反”的概率是 $\text{[math]}$ B . 事件“两个正数相加，和是正数”是必然事件 C . 数2和8的比例中项是4 D . 同一张底片洗出来的两张照片是位似图形

答案解析收藏纠错 + 选题
4. (2024九上·杭州期中) 已知⊙O的半径为5，点P在⊙O外，则OP的长可能是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
5. (2021九上·萧山月考) 如图，已知AB为⊙O的直径，C，D是圆上AB同侧的两点，∠ACD＝120°，则∠BAD＝（　　）

A . 50° B . 40° C . 30° D . 20°

答案解析收藏纠错 + 选题
6. (2021九上·萧山月考) 已知二次函数y＝ax²+bx+1的图象与x轴没有交点，且过点A（﹣2，y₁），B（﹣3，y₂），C（1，y₂），D（ $\text{[math]}$ ，y₃），则y₁ ， y₂ ， y₃的大小关系是（　　）

A . y₂＞y₁＞y₃ B . y₃＞y₂＞y₁ C . y₁＞y₃＞y₂ D . y₁＞y₂＞y₃

答案解析收藏纠错 + 选题
7. (2021九上·萧山月考) 如图，在△ABC中，点D，E分别是AC和BC的中点，连接AE，BD交于点F，则下列结论中正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
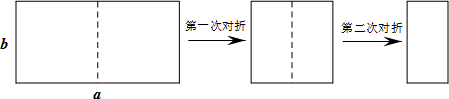
8. (2021九上·拱墅月考) 如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（）

A . a＝ $\text{[math]}$ b B . a＝2b C . a＝2 $\text{[math]}$ b D . a＝4b

答案解析收藏纠错 + 选题
9. (2021九上·萧山月考) 设直线x＝1是函数y＝ax²+bx+c（a，b，c是实数，且a＜0）的图象的对称轴，（）

A . 若m＞1，则（m﹣1）a+b＞0 B . 若m＞1，则（m﹣1）a+b＜0 C . 若m＜1，则（m+1）a+b＞0 D . 若m＜1，则（m+1）a+b＜0

答案解析收藏纠错 + 选题
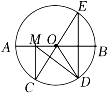
10. (2021九上·萧山月考) 如图，在⊙O中，AB是⊙O的直径，OB＝5， $\text{[math]}$ ＝ $\text{[math]}$ ＝ $\text{[math]}$ ，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：① $\text{[math]}$ 的长度是 $\text{[math]}$ ；②∠CED＝ $\text{[math]}$ ∠DOB；③DM⊥CE；④CM+DM的最小值是10，上述结论中正确的个数是（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、认真填一填（本题有6个小题，每小题4分，共24分）

11. (2021九上·萧山月考) 已知抛物线y＝（x+1）²向右平移2个单位，再向上平移1个单位，得到的抛物线表达式为.

答案解析收藏纠错 + 选题

12. (2021九上·萧山月考) 在一个不透明的口袋里装有仅颜色不同100个球，某小组做摸球试验，将球搅匀后从中随机摸出1个球，记下颜色，再把它放回，不断重复，下表是试验中记下的一组数据：

摸球的次数n	100	150	200	500	800	1000
摸到红球的次数m	79	115	152	385	598	751
摸到红球的频率 $\text{[math]}$	0.790	0.767	0.760	0.770	0.748	0.751

试估计口袋中红球有个.

答案解析收藏纠错 + 选题

13. (2021九上·萧山月考) 已知：点C是线段AB的黄金分割点，AB=2，则AC=．

答案解析收藏纠错 + 选题
14. (2021九上·萧山月考) 如图，在半径为13的⊙O中，AB，CD是互相垂直的两条弦，垂足为P，且AB＝CD＝24，则OP的长是.

答案解析收藏纠错 + 选题
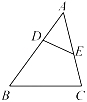
15. (2021九上·萧山月考) 在△ABC中，点D、E分别在AB、AC上，∠AED＝∠B，如果AB＝2，△ADE的面积为4，四边形BCED的面积为5，那么AE的长为 .

答案解析收藏纠错 + 选题
16. (2021九上·萧山月考) 二次函数 $\text{[math]}$ ，当2m﹣3≤x≤2m时，y的最小值是1，则m的值是.

答案解析收藏纠错 + 选题

三、全面答一答（本题有7个小题，共66分）解答应写出文字说明、证明过程或推演步骤.

17. (2022九上·杭州月考) 防疫期间，全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道，某天早晨，该校小明和小丽两位同学将随机通过测温通道进入校园.
1. （1）小明从A测温通道通过的概率是；
2. （2）利用画树状图或列表的方法，求小明和小丽从同一个测温通道通过的概率.
答案解析收藏纠错 + 选题
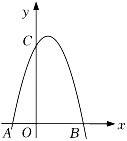
18. (2021九上·萧山月考) 如图，已知抛物线y＝﹣x²+bx+c与坐标轴交于A，B，C三点，其中A（﹣2，0），B（4，0）.
1. （1）求该抛物线的表达式和顶点坐标；
2. （2）直接写出当y＜0时，x的取值范围.
答案解析收藏纠错 + 选题
19. (2021九上·萧山月考) 如图，在△ABC中，AB＝AC，E在AC上，经过A，B，E三点的圆O交BC于点D，且D点是 $\text{[math]}$ 的中点.
1. （1）求证：AB是圆的直径；
2. （2）若AB＝8，∠C＝60°，求阴影部分的面积.
答案解析收藏纠错 + 选题
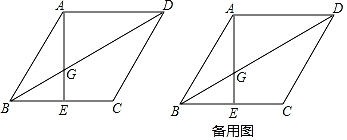
20. (2021九上·萧山月考) 如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE＝ED，DF＝ $\text{[math]}$ DC，连接EF并延长交BC的延长线于点G.
1. （1）求证： $\text{[math]}$ ；
2. （2）若正方形的边长为4，求FG的长.
答案解析收藏纠错 + 选题
21. (2022九上·杭州月考) 如图，AB是⊙O的直径，弦CD⊥AB于点E，G是 $\text{[math]}$ 上一点，AG，DC的延长线交于点F，连接AD，GD，GC.
1. （1）求证：∠ADG＝∠F；
2. （2）已知CD＝6，BE＝2，求⊙O的半径长.
答案解析收藏纠错 + 选题
22. (2021九上·萧山月考) 已知二次函数y＝（x+1）（x+3k）.
1. （1）若当x＝1时，该函数有最小值，求k的值.
2. （2）若二次函数图象向上平移1个单位后与x轴只有一个交点，求k的值.
3. （3）已知k≥1，当x≥m时，y随着x的增大而增大，试求出m的一个值.
答案解析收藏纠错 + 选题
23. (2021九上·萧山月考) 如图，在菱形ABCD中，点E在BC边上（与点B、C不重合），连接AE交BD于点G.
1. （1）若AG＝BG，AB＝2，BD＝3，求线段DG的长；
2. （2）设BC＝kBE，△BGE的面积为S，△AGD和四边形CDGE的面积分别为S₁和S₂ ，把S₁和S₂分别用k、S的代数式表示；
3. （3）求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题