
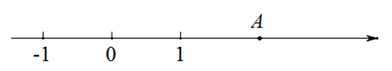
①用直尺和圆规在数轴上作出表示实数的 的点P;(保留作图痕迹,不写作法)
②利用数轴比较 和a的大小,并说明理由.
……第一步
……第二步
……第三步
……第四步
任务一:以上化简步骤中第一步化简的依据是:;
任务二:第步开始出现错误,请写出错误的原因,该试运算正确结果是.
解决问题:
①当 ,
,则
;
② (
且
为整数).
在进行二次根式的化简与计算时我们有时会遇到如: ,
这样的式子,其实我们还可以将其进一步化简:
=
=
;
=
=
=
.
以上将分母中的根号化去的过程,叫做分母有理化.
请参照以上方法化简下列各式:
例:若代数式 ,求a的取值.
解:原式=|a﹣2|+|a﹣4|,
当a<2时,原式=(2﹣a)+(4﹣a)=6﹣2a=2,解得a=2(舍去);
当2≤a<4时,原式=(a﹣2)+(4﹣a)=2,等式恒成立;
当a≥4时,原式=(a﹣2)+(a﹣4)=2a﹣6=2,解得a=4;
所以,a的取值范围是2≤a≤4.
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题: