 B .
B .  C .
C .  D .
D . 





求:
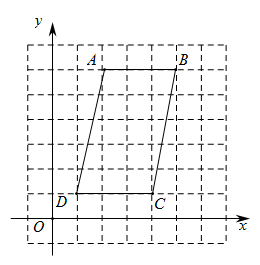
⑴将线段AD绕点A逆时针旋转90°,画出对应线段AE,并直接写出点E的坐标 ▲▲ ;
⑵过(1)中点E画一条直线把平行四边形ABCD分成面积相等的两部分;
⑶找一个格点F,使得CF⊥AD,并直接写出点F的坐标 ▲ .
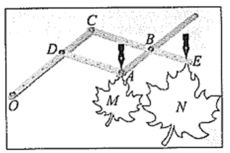
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点, ,
, 在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接 ,
, 可证得以下结论:
①和
为等腰三角形,则
,
(180°-∠ ▲ );
②四边形为平行四边形(理由是 ▲ );
③ , 于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.






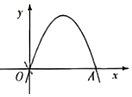
如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a=,点A的坐标为.
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式:.
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是.
如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
①求A、B两点的坐标;(用含h的式子表示)
②当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.