2022年初中数学浙教版八年级下册2.3一元二次方程的应用能...

更新时间：2022-01-18 浏览次数：144 类型：同步测试

一、单选题

1. (2015九上·黄陂期中) 电脑病毒传播快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染，若每轮感染中平均一台电脑会感染x台电脑，下列方程正确的是（　）

A . x（x+1）=81 B . 1+x+x²=81 C . 1+x+x（x+1）=81 D . 1+（x+1）²=81

答案解析收藏纠错 + 选题
2. 要组织一次篮球邀请赛，参赛的每两个队之间都要比赛一场，据场地和时间等条件的限制，赛程计划安排7天，每天安排4场比赛，刚好完成所有比赛．设比赛组织者邀请x个队参赛，则根据题意所列方程正确的是（　　）

A . $\text{[math]}$ x（x+1）=28 B . $\text{[math]}$ x（x﹣1）=28 C . x（x+1）=28 D . x（x﹣1）=28

答案解析收藏纠错 + 选题
3. 某商品经过两次降价，零售价降为原来的 $\text{[math]}$ ，已知两次降价的百分率均为x，则列出方程正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . （1+x）²=2 D . （1﹣x）²=2

答案解析收藏纠错 + 选题
4. (2020九上·丰宁期末) 某口罩生产厂2020年1月份平均日产20万个，1月底因防控新冠疫情需求，工厂立即决定从2月份起扩大产能，3月份平均日产量达到45万个，则口罩日产量的月平均增长率是（）

A . 20% B . 30% C . 40% D . 50%

答案解析收藏纠错 + 选题
5. (2019八下·温州期末) 《代数学》中记载，形如x²+10x=39的方程，求正数解的几何方法是：“如图1，先构造一个面积为x²的正方形，再以正方形的边长为一边向外构造四个面积为 $\text{[math]}$ x的矩形，得到大正方形的面积为39+25=64，则该方程的正数解为8-5=3”，小聪按此方法解关于x的方程x²+6x+m=0时，构造出如图2所示的图形，已知阴影部分的面积为36，则该方程的正数解为（）

A . 6 B . 3 $\text{[math]}$ -3 C . 3 $\text{[math]}$ -2 D . 3 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

6. (2021八上·松江期中) 某工厂4月份的产值为100万元，之后每个月的增长率不变，若第二季度的总产值为364万元，设每月的增长率为 $\text{[math]}$ ，则可列方程为．

答案解析收藏纠错 + 选题
7. (2023九上·遵义月考) 一个两位数，十位上的数字比个位上的数字的平方少9.如果把十位上的数字与个位上的数字对调，得到的两位数比原来的两位数小27，则原来的两位数是

答案解析收藏纠错 + 选题
8. (2017八下·射阳期末) 要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则可列一元二次方程为．（化用一般式表示）

答案解析收藏纠错 + 选题
9. (2020八下·温州期中) 某服装店经销一种品牌服装，平均每天可销售20件，每件赢利44元，经市场预测发现：在每件降价不超过10元的情况下，若每件降价1元，则每天可多销售5件，若该专卖店要使该品牌服装每天的赢利为1600元，则每件应降价____元．

答案解析收藏纠错 + 选题
10. (2022·峨边模拟)
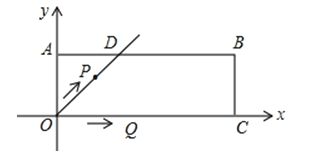
在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒 $\text{[math]}$ 个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒，当t为时，△PQB为直角三角形．

答案解析收藏纠错 + 选题

三、综合题

11. (2021八下·苍南期末) 用总长700cm的木板制作矩形置物架ABCD (如图)，已知该置物架上面部分为正方形ABFE，下面部分是两个全等的矩形DGMN和矩形CNMH，中间部分为矩形EFHG。已知DG=60cm，设正方形的边长AB=x (cm)。
1. （1）当x=75时，EG的长为cm
2. （2）置物架ABCD的高AD的长为cm (用含x的代数式表示)
3. （3）为了便于置放物品，EG的高度不小于26cm，若矩形ABCD的面积为12750 (cm²)，求x的值。
答案解析收藏纠错 + 选题

12. (2021八下·温州期末) 为响应国家“垃圾分类"的号召，温州市开始实施《城镇垃圾分类标准》，某商场向厂家订购了A，B两款垃圾桶共100个。已知购买A款垃圾桶个数不超过30个时，每个A款垃圾桶进价为80元，若超过30个时，每增加1个垃圾桶，进价减少2元，厂家为保障盈利，每个A款垃圾桶进价不低于50元。每个B款垃圾桶的进价为40元，设所购买A款垃圾桶的个数为x个。

（1）根据信息填表：

款式	数量（个）	进价（元/个）
A	x（不超过30个时）	80
A	x （超过30个时）
B		40

（2）若订购的垃圾桶的总进价为4800元，则该商场订购了多少个A款垃圾桶？

答案解析收藏纠错 + 选题

13. (2021九上·于洪期中) 某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，以扩大销售量，尽快减少库存，增加利润.经市场调查发现，如果每件童装降价1元，那么平均可多售出2件.
1. （1）设每件童装降价 $\text{[math]}$ 元时，每天可销售件，每件盈利元；（用 $\text{[math]}$ 的代数式表示）
2. （2）为了扩大销售量，尽快减少库存，每件童装降价多少元时，平均每天赢利1200元；
3. （3）平均每天赢利1300元，可能吗？请说明理由.
答案解析收藏纠错 + 选题
14. (2021九上·武汉月考) 科学研究表明接种疫苗是战胜新冠病毒的最有效途径.当前居民接种疫苗迎来高峰期，导致相应医疗物资匮乏，某工厂及时补进了一条一次性注射器生产线生产一次性注射器.开工第一天生产200万个，第三天生产288万个.试回答下列问题：
1. （1）求前三天生产量的日平均增长率；
2. （2）经调查发现，1条生产线最大产能是600万个/天，若每增加 $\text{[math]}$ 条生产线，每条生产线的最大产能将减少20万个/天.
  ①现该厂要保证每天生产一次性注射2600万个，在增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？
  
  ②是否能增加生产线，使得每天生产一次性注射器5000万个，若能，应该增加几条生产线？若不能，请说明理由.
答案解析收藏纠错 + 选题
15. (2024八下·杭州期中) 某农场要建一个饲养场（矩形ABCD），两面靠墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图所示的三处各留1米宽的门（不用木栏）.建成后木栏总长45米.
1. （1）若饲养场（矩形ABCD）的一边CD长为8米，则另一边BC＝米.
2. （2）若饲养场（矩形ABCD）的面积为180平方米，求边CD的长.
3. （3）饲养场的面积能达到210平方米吗？若能达到，求出边CD的长；若不能达到，请说明理由.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2022年初中数学浙教版八年级下册2.3一元二次方程的应用能...

副标题：

*注意事项：

2022年初中数学浙教版八年级下册2.3一元二次方程的应用能...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析