江苏省宜兴市树人中学教育集团2021-2022学年九年级上学...

更新时间：2022-03-11 浏览次数：78 类型：月考试卷

一、单选题

1. (2021九上·宜兴月考) 下列方程中是一元二次方程的是（）

A . -5x+2=1 B . 2x²-y+1=0 C . x²+2x=0 D . $\text{[math]}$ +x=2

答案解析收藏纠错 + 选题
2. (2021九上·宜兴月考) 若△ABC∽△A'B'C'，∠A＝30°，∠C＝110°，则∠B'的度数为（）

A . 30° B . 50° C . 40° D . 70°

答案解析收藏纠错 + 选题
3. (2021九上·宜兴月考) 已知线段a、b、c，其中c的长度是a、b长度的比例中项，若a＝9cm，b＝4cm，则线段c的长为（）

A . 5cm B . 6cm C . 18cm D . ±6cm

答案解析收藏纠错 + 选题
4. (2021九上·宜兴月考) 若二次函数y＝x²－6x＋c的图象过A（－1，y₁）、B（2，y₂）、C（5，y₃）三点，则y₁、y₂、y₃的大小关系正确的是（）

A . y₁＞y₂＞y₃ B . y₁＞y₃＞y₂ C . y₂＞y₁＞y₃ D . y₃＞y₁＞y₂

答案解析收藏纠错 + 选题
5. (2021九上·宜兴月考) 如图 $\text{[math]}$ 是 $\text{[math]}$ 切线，点A为切点， $\text{[math]}$ 交 $\text{[math]}$ 于点C，点D在 $\text{[math]}$ 上，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 25° B . 20° C . 30° D . 35°

答案解析收藏纠错 + 选题
6. (2022八下·台江期末) 要组织一次篮球联赛，赛制为单循环形式，每两队之间都赛一场，计划安排15场比赛.设比赛组织者应邀请x个队参赛，则x满足的关系式为（）

A . $\text{[math]}$ x（x﹣1）＝15 B . $\text{[math]}$ x（x+1）＝15 C . x（x+1）＝15 D . x（x﹣1）＝15

答案解析收藏纠错 + 选题
7. (2021九上·宜兴月考) 如图，△ABC中，AB＝AC，∠BAC＝70°，⊙O是△ABC的外接圆，点D在劣弧 $\text{[math]}$ 上，则∠D的度数是（）

A . 55° B . 110° C . 125° D . 140°

答案解析收藏纠错 + 选题
8. (2021九上·宜兴月考) 下列说法：①三点确定一个圆；②同弧所对的圆周角度数相等；③90°的角所对的弦是直径；④圆的切线垂直于半径；⑤三角形的外心到三角形的三个顶点的距离相等.其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2021九上·宜兴月考) 如图，点E在y轴上，⊙E与x轴交于点A、B，与y轴交于点C、D，若C（0，16），D（0，﹣4），则线段AB的长度为（）

A . 10 B . 8 C . 20 D . 16

答案解析收藏纠错 + 选题
10. (2021九上·河南月考) 如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x²+2x+1与y轴交于点C，点E在抛物线y=﹣x²+2x+1的对称轴上移动，点F在直线AB上移动，CE+EF的最小值是（）

A . 1.4 B . 2.5 C . 2.8 D . 3

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·宜兴月考) 若关于x的一元二次方程kx²﹣2x﹣1=0有两个不相等的实数根，则实数k的取值范围是．

答案解析收藏纠错 + 选题
12. (2021九上·宜兴月考) 如果在比例尺为1：1000000的地图上，A、B两地的图上距离是5.8cm，那么A、B两地的实际距离是km.

答案解析收藏纠错 + 选题
13. (2021九上·宜兴月考) 在平行四边形ABCD中，E为靠近点D的AD的三等分点，连结BE，交AC于点F，AC＝12，则AF为.

答案解析收藏纠错 + 选题
14. (2021九上·宜兴月考) 在正五边形的外接圆中，任一边所对的圆周角的度数为.

答案解析收藏纠错 + 选题
15. (2021九上·宜兴月考) 如图，AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q．若AB＝2，则线段BQ的长为.

答案解析收藏纠错 + 选题
16. (2021九上·宜兴月考) 圆锥的高为4cm，底面圆的半径长为3cm，则该圆锥的侧面积为cm²

答案解析收藏纠错 + 选题
17. (2021九上·宜兴月考) 如图，平行于 $\text{[math]}$ 轴的直线 $\text{[math]}$ 分別交函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象于 $\text{[math]}$ 、 $\text{[math]}$ 两点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，直线DE $\text{[math]}$ AC，交 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2021九上·宜兴月考) 在等边△ABC中，AB＝6，BD＝4，点E为AC边上一个动点，连接DE，将△CDE沿着DE翻折得到△FDE，则点F到AB距离的最小值是.

答案解析收藏纠错 + 选题

三、解答题

19. (2021九上·宜兴月考) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ；
3. （3） $\text{[math]}$ （配方法）；
4. （4） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2023九上·淮南月考) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有实数根．
1. （1）求 $\text{[math]}$ 的取值范围；
2. （2）如果 $\text{[math]}$ 是符合条件的最大整数，且一元二次方程 $\text{[math]}$ 与方程 $\text{[math]}$ 有一个相同的根，求此时 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
21. (2021九上·宜兴月考) 如图，已知在△ABC中，∠A=90°.
1. （1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）；
2. （2）在（1）的条件下，若∠B=45°，AB=1，⊙P切BC于点D，求劣弧 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
22. (2021九上·宜兴月考) 如图，已知二次函数y＝-x²+ax+1的图象经过点P（2，1）.
1. （1）求a的值和图象的顶点坐标.
2. （2）点Q（m，n）在该二次函数图象上，
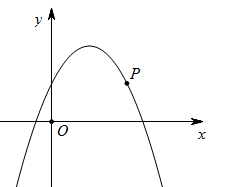
  ①当m＝3时，求n的值；
  
  ②若点Q到y轴的距离小于2，请根据图象直接写出n的取值范围.
答案解析收藏纠错 + 选题
23. (2021九上·宜兴月考) 如图，在边长为1小正方形的网格中，△ABC的顶点A、B、C均落在格点上，请用无刻度的直尺按要求作图.（保留画图痕迹，请将经过的格点描重一点，不需证明）
1. （1）如图1，点P在格点上，在线段AB上找出所有符合条件的点Q，使△APQ和△ABC相似；
2. （2）如图2，在AB上找点Q，使BQ＝3，并求此时CQ的长为.
答案解析收藏纠错 + 选题
24. (2022九上·铜梁开学考) 为了测量学校旗杆的高度AB，数学兴趣小组带着标杆和皮尺来到操场进行测量，测量方案如下：如图，首先，小红在C处放置一平面镜，她从点C沿BC后退，当退行1.8米到D处时，恰好在镜子中看到旗杆顶点A的像，此时测得小红眼睛到地面的距离ED为1.5米；然后，小明在F 处竖立了一根高1.6米的标杆FG，发现地面上的点H、标杆顶点G和旗杆顶点A在一条直线上，此时测得FH为2.4米，DF为3.3米，已知AB⊥BH，ED⊥BH，GF⊥BH，点B、C、D、F、H在一条直线上.
1. （1）直接写出 $\text{[math]}$ ；
2. （2）请根据以上所测数据，计算学校旗杆AB的高度.
答案解析收藏纠错 + 选题
25. (2021九上·宜兴月考) “新冠”疫情蔓延全球，口罩成了人们的生活必需品.某药店销售普通口罩和N95口罩，今年8月份的进价如表：

普通口罩

N95口罩

进价（元/包）

8

20
1. （1）计划N95口罩每包售价比普通口罩贵16元，7包普通口罩和3包N95口罩总售价相同，求普通口罩和N95口罩每包售价；
2. （2）按（1）中售价销售一段时间后，发现普通罩的日均销售量为120包，当每包售价降价0.5元时，日均销售量增加10包.该药店秉承让利于民的原则，对普通口罩进行降价销售，但要保证当天的利润为320元，求此时普通口罩每包售价；
3. （3）疫情期间，该药店进货2万包N95口罩，进价不变，店长向当地医院捐赠了a包（6000≤a≤7000）该款口罩，剩余的N95口罩向市民销售.若这2万包口罩的利润率等于10%，求N95口罩每包售价.（售价为整数元）
答案解析收藏纠错 + 选题
26. (2021九上·宜兴月考) 如图，在Rt△ABC中，∠C＝90°，AC＝8cm，BC＝6cm.现在有动点P从点B出发，沿线段BA向终点A运动，动点Q从点A出发，沿折线AC—CB向终点运动.如果点P的速度是1cm/s，点Q的速度是1cm/s.它们同时出发，当有一点到达终点时，另一点也停止运动.设运动的时间为t秒.
1. （1）如图1，Q在AC上，当t为多少秒时，以点A、P、Q点的三角形与 $\text{[math]}$ 相似？
2. （2）如图2，Q在CB上，否存着某时刻，使得以点B、P、Q顶点的三角形与 $\text{[math]}$ 相似？若存在，求出t的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
27. (2021九上·宜兴月考) 如图直角坐标系中，以M（3，0）为圆心的⊙M交x轴负半轴于A，交x轴正半轴于B，交y轴于C、D.
1. （1）若C点坐标为（0，4），求点A坐标.
2. （2）在（1）的条件下，在⊙M上，是否存在点P，使∠CPM=45°，若存在，求出满足条件的点P.
3. （3）过C作⊙M的切线CE，过A作AN⊥CE于F，交⊙M于N，当⊙M的半径大小发生变化时.AN的长度是否变化？若变化，求变化范围，若不变，证明并求值.
答案解析收藏纠错 + 选题
28. (2023·雷州模拟) 如图1，二次函数y=ax²﹣2ax﹣3a（a＜0）的图象与x轴交于A、B两点（点A在点B的右侧），与y轴的正半轴交于点C，顶点为D.
1. （1）求顶点D的坐标（用含a的代数式表示）.
2. （2）若以AD为直径的圆经过点C.
  ①求a的值.
  
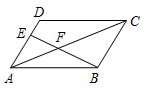
  ②如图2，点E是y轴负半轴上一点，连接BE，将△OBE绕平面内某一点旋转180°，得到△PMN（点P、M、N分别和点O、B、E对应），并且点M、N都在抛物线上，作MF⊥x轴于点F，若线段BF=2MF，求点M、N的坐标.
  
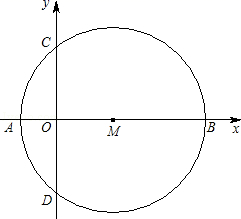
  ③如图3，点Q在抛物线的对称轴上，以Q为圆心的圆过A、B两点，并且和直线CD相切，求点Q的坐标.
答案解析收藏纠错 + 选题