题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

北京市顺义区2021-2022学年九年级上学期期末数学试题

更新时间：2024-07-13 浏览次数：143 类型：期末考试

一、单选题

1. (2021九上·顺义期末) 如果 $\text{[math]}$ （ $\text{[math]}$ ），那么下列比例式中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九上·拱墅期末) 如图，在平面直角坐标系内有一点P（3，4），连接OP，则OP与x轴正方向所夹锐角α的正弦值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·伊春期中) 将抛物线y=3x²向左平移2个单位后得到的抛物线的解析式为（　　）

A . y=3（x+2）² B . y=3（x-2）² C . y=3x²+2 D . y=3x²-2

答案解析收藏纠错 + 选题
4. (2021九上·顺义期末) 如图是拦水坝的横断面，斜坡AB的水平宽度为12米，斜面坡度为1：2，则斜坡AB的长为（）米

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 24

答案解析收藏纠错 + 选题
5. (2021九上·顺义期末) 如图，点D在△ABC的边AC上，要判断△ADB与△ABC相似，添加一个条件，错误的是（）

A . ∠ABD=∠C B . ∠ADB=∠ABC C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·顺义期末) 如图，AB切于⊙O点B，延长AO交⊙O于点C，连接BC，若∠A=40°，则∠C=（）

A . 20° B . 25° C . 40° D . 50°

答案解析收藏纠错 + 选题
7. (2021九上·顺义期末) 如图，在 $\text{[math]}$ 中，如果 $\text{[math]}$ ＝2 $\text{[math]}$ ，则下列关于弦AB与弦AC之间关系正确的是（）

A . AB＝AC B . AB＝ 2AC C . AB ＞2AC D . AB ＜ 2AC

答案解析收藏纠错 + 选题
8. (2024九下·海口模拟) 已知点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上.若 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·永寿期末) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是.

答案解析收藏纠错 + 选题
10. (2021九上·顺义期末) 若二次函数 $\text{[math]}$ 配方后为 $\text{[math]}$ ，则b＝， k＝．

答案解析收藏纠错 + 选题
11. (2021九上·顺义期末) 如图，身高是1.6m的某同学直立于旗杆影子的顶端处，测得同一时刻该同学和旗杆的影子长分别为1.2m和9m.则旗杆的高度为m.

答案解析收藏纠错 + 选题
12. (2021九上·顺义期末) 如图，在 $\text{[math]}$ 中，D，E分别是边 $\text{[math]}$ ， $\text{[math]}$ 的中点，则 $\text{[math]}$ 与 $\text{[math]}$ 的周长之比等于.

答案解析收藏纠错 + 选题
13. (2021九上·顺义期末) 在矩形ABCD中，BC=6，CD=8，以A为圆心画圆，且点D在⊙A内，点B在⊙A外，则⊙A半径r的取值范围是．

答案解析收藏纠错 + 选题
14. (2021九上·顺义期末) 如图，正六边形ABCDEF内接于半径为3的⊙O ，则劣弧AB的长度为．

答案解析收藏纠错 + 选题
15. (2022·河南模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
16. (2022·昆明模拟) 如图，两个反比例函数 $\text{[math]}$ 和 $\text{[math]}$ 在第一象限内的图象分别是C₁和C₂ ，设点P在C₁上，PA⊥x轴于点A，交C₂于点B，则△POB的面积为．

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·顺义期末) 解不等式组 $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021九上·顺义期末) 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
19. (2021九上·顺义期末) 已知：如图，锐角∠AOB．
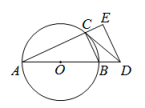
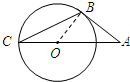
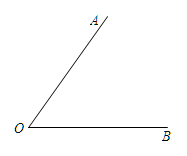
求作：射线OP，使OP平分∠AOB．
作法：
①在射线OB上任取一点M；
②以点M为圆心，MO的长为半径画圆，分别交射线OA，OB于C，D两点；
③分别以点C，D为圆心，大于 $\text{[math]}$ 的长为半径画弧，在∠AOB内部两弧交于点H；
④作射线MH，交⊙M于点P；
⑤作射线OP．
射线OP即为所求．
1. （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
2. （2）完成下面的证明．
  证明：连接CD．
  由作法可知MH垂直平分弦CD．
  ∴ $\text{[math]}$ （ ▲ ）（填推理依据）．
  ∴∠COP ＝ ▲ ．
  即射线OP平分∠AOB．
答案解析收藏纠错 + 选题
20. (2022九上·金东月考) 如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB.
1. （1）求证：△BDE∽△EFC.
2. （2）设 $\text{[math]}$ ，
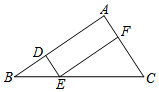
  ①若BC＝12，求线段BE的长；
  
  ②若△EFC的面积是20，求△ABC的面积.
答案解析收藏纠错 + 选题
21. (2022九上·昌平期中) 如图，在矩形ABCD中，E为BC的中点，DF⊥AE ，垂足为F，AB＝6，BC＝4，求AE，DF的长．

答案解析收藏纠错 + 选题
22. (2021九上·顺义期末) 如图，为了测量某条河的宽度，在河边的一岸边任意取一点A，又在河的另一岸边取两点B、C，测得∠α＝30°，∠β＝60°，量得BC长为100米．求河的宽度（结果保留根号）．

答案解析收藏纠错 + 选题
23. (2021九上·顺义期末) 如图，△ABC内接于⊙O，AB是⊙O的直径，作∠BCD＝∠A，CD与AB的延长线交于点D，DE⊥AC，交AC的延长线于点E．
1. （1）求证：CD是⊙O的切线；
2. （2）若CE＝2，DE＝4，求AC的长．
答案解析收藏纠错 + 选题
24. (2021九上·顺义期末) 如图，一小球沿与地面成一定角度的方向飞出，小球的飞行路线是一条抛物线，如果不考虑空气阻力，小球的飞行高度y（单位：m）与飞行时间x（单位：s）之间具有函数关系y=﹣5x²+20x，请根据要求解答下列问题：
1. （1）在飞行过程中，当小球的飞行高度为15m时，飞行时间是多少？
2. （2）在飞行过程中，小球从飞出到落地所用时间是多少？
3. （3）在飞行过程中，小球飞行高度何时最大？最大高度是多少？
答案解析收藏纠错 + 选题
25. (2022九下·普陀月考) 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ ， $\text{[math]}$ 两点.
1. （1）求一次函数和反比例函数的解析式；
2. （2）点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，且满足 $\text{[math]}$ 的面积等于4，请直接写出点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
26. (2021九上·顺义期末) 已知抛物线 $\text{[math]}$ 经过点M（﹣1，1），N（2，﹣5）．
1. （1）求a，b的值；
2. （2）若P（4， $\text{[math]}$ ），Q（ $\text{[math]}$ ， $\text{[math]}$ ）是抛物线上不同的两点，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
27. (2021九上·顺义期末) 已知抛物线 $\text{[math]}$ ．
1. （1）求证：该抛物线与x轴有两个交点；
2. （2）求出它的交点坐标（用含m的代数式表示）；
3. （3）当两交点之间的距离是4时，求出抛物线的表达式．
答案解析收藏纠错 + 选题
28. (2022·雨山模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，D是AB上一点，⊙O经过点A、C、D，交BC于点E，过点D作 $\text{[math]}$ ，交⊙O于点F，求证：
1. （1）四边形DBCF是平行四边形
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
29. (2021九上·顺义期末) 如图，△ABC内接于⊙O，AB为⊙O的直径，AB＝5，AC＝3．
1. （1）求tanA的值；
2. （2）若D为 $\text{[math]}$ 的中点，连接CD、BD，求弦CD的长．
答案解析收藏纠错 + 选题

试卷信息