2022年初中数学浙教版七下第四章因式分解能力阶梯训练——...

更新时间：2022-03-07 浏览次数：153 类型：单元试卷

一、单选题

1. (2021八上·平原月考) 下列因式分解正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八上·余杭开学考) 下列等式从左到右的变形，属于因式分解的是（）

A . m （a+b）＝ma+mb B . x²+2x+1＝x（x+2）+1 C . x²+x＝x²（1+ $\text{[math]}$ ） D . x²﹣9＝（x+3）（x﹣3）

答案解析收藏纠错 + 选题
3. (2021八上·安次月考) 已知多项式 $\text{[math]}$ 是一个完全平方式，则 $\text{[math]}$ 的值是（）

A . -7 B . -17 C . 15 D . 15或-17

答案解析收藏纠错 + 选题
4. (2024七下·桂林月考) 当n为自然数时，（n+1）²﹣（n﹣3）²一定能（）

A . 被5整除 B . 被6整除 C . 被7整除 D . 被8整除

答案解析收藏纠错 + 选题
5. (2023八上·东平月考) 下列各式中，没有公因式的是（）

A . 3x﹣2与6x²﹣4x B . ab﹣ac与ab﹣bc C . 2（a﹣b）²与3（b﹣a）³ D . mx﹣my与ny﹣nx

答案解析收藏纠错 + 选题
6. (2021八上·沂源期中) 将多项式 $\text{[math]}$ 加上一个单项式后，使它能成为另一个整式的完全平方，下列添加单项式错误的是（）

A . 4x B . $\text{[math]}$ ⁴ C . $\text{[math]}$ ⁴ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021八上·招远期中) 下列各式能用完全平方公式进行因式分解的是（）

A . 9x²-6x+1 B . x²+x+1 C . x²+2x-1 D . x²-9

答案解析收藏纠错 + 选题
8. (2021八上·泰安期中) 计算-2²⁰²¹+(-2)²⁰²⁰所得的结果是（）

A . -2²⁰²⁰ B . -2²⁰²¹ C . 2²⁰²⁰ D . -2

答案解析收藏纠错 + 选题
9. (2021八上·德阳月考) 若一个三角形的三边长为a，b，c，且满足a²-2ab+b²+ac-bc =0，则这个三角形是（）

A . 直角三角形 B . 等边三角形 C . 等腰三角形 D . 等腰直角三角形

答案解析收藏纠错 + 选题
10. (2021八上·德阳月考) 若一个等腰三角形的两边m，n满足9m²-n²=-13，3m+n=13，则该等腰三角形的周长为（）

A . 11 B . 13 C . 16 D . 11或16

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·八步模拟) 因式分解：x²－36= .

答案解析收藏纠错 + 选题
12. (2021·仙桃) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2021九上·陕西开学考) 因式分解：m³n﹣4m²n²+4mn³＝.

答案解析收藏纠错 + 选题
14. (2022八上·霍林郭勒期末) 分解因式 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024七下·西安月考) 若 $\text{[math]}$ 是完全平方式，则m＝．

答案解析收藏纠错 + 选题
16. (2023七下·桐乡市月考) 已知长方形的长、宽分别为x，y，周长为12，面积为4，则x²+y²的值是．

答案解析收藏纠错 + 选题

三、综合题

17. (2021八上·拜泉期中) 因式分解
1. （1） 6x²﹣3x；
2. （2） 16m³﹣mn²；
3. （3） 25m²﹣10mn+n²；
4. （4） 9a²（x﹣y）+4b²（y﹣x）．
答案解析收藏纠错 + 选题
18. (2021八上·陇县期末) 分解因式
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. 先阅读，再解答下列问题.
已知（a²+b²）-8（a²+b²）²+16=0，求a²+b²的值.

错解：设（a²+b²）²=m，

则原式可化为m²-8m+16=0，

即（m-4）²=0，解得m=4.

由（a²+b²）²=4，得a²+b²=±2
1. （1）上述解答过程错在哪里？为什么？
2. （2）请你用上述方法分解因式：（a+b）²-14（a+b）+49
答案解析收藏纠错 + 选题
20. 配方法是数学中一种重要的思想方法，利用完全平方公式，可将 $\text{[math]}$ 配方成 $\text{[math]}$ 的形式，即 $\text{[math]}$ ．
（解决问题）
1. （1）利用配方法将 $\text{[math]}$ 化成 $\text{[math]}$ 的形式后， $\text{[math]}$ ， $\text{[math]}$ ．
2. （2）求证：不论 $\text{[math]}$ 、 $\text{[math]}$ 取任何实数，多项式 $\text{[math]}$ 的值总为正数．
答案解析收藏纠错 + 选题
21. (2017七下·常州期中)
教材中，在计算如图1所示的正方形ABCD的面积时，分别从两个不同的角度进行了操作：

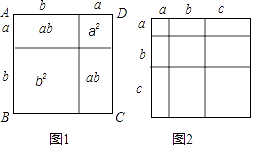
（i）把它看成是一个大正方形，则它的面积为（a+b）²；

（ii）把它看成是2个小长方形和2个小正方形组成的，则它的面积为a²+2ab+b²；因此，可得到等式：（a+b）²=a²+2ab+b² ．
1. （1）类比教材中的方法，由图2中的大正方形可得等式：．
2. （2）
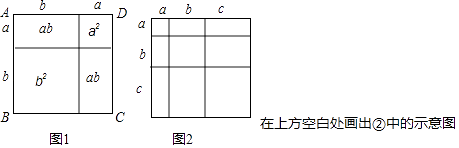
  试在图2右边空白处画出面积为2a²+3ab+b²的长方形的示意图（标注好a，b），由图形可知，多项式2a²+3ab+b²可分解因式为：．
3. （3）若将代数式（a₁+a₂+a₃+…+a₂₀）²展开后合并同类项，得到多项式N，则多项式N的项数一共有项．
答案解析收藏纠错 + 选题
22. (2021八上·泰安期中) 第一环节：自主阅读材料：
常用的分解因式方法有提公因式、公式法等．但有的多项式只用上述方法就无法分解，如x²-4y²+2x-4y，细心观察这个式子会发现前两项符合平方差公式，后两项可提取公因式，分解过程为：

x²-4y²+2x-4y

=(x²-4y²)+(2x-4y) ……分组

=(x-2y)(x+2y)+2(x-2y) ……组内分解因式

=(x-2y)(x+2y+2) ……整体思想提公因式

这种分解因式的方法叫分组分解法。

第二环节：利用这种方法解决下列问题。

因式分解：x²y-4y-2x²+8．

第三环节：拓展运用。

已知a，b，c为△ABC的三边，且b²+2ab=c²+2ac，试判断△ABC的形状．

答案解析收藏纠错 + 选题
23. (2021八上·密山期末) 先阅读下列材料：我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等．
拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法．如：
x²＋2x﹣3＝x²＋2x＋1﹣4＝（x＋1）²﹣2²＝（x＋1＋2）（x＋1﹣2）＝（x＋3）（x﹣1）
请你仿照以上方法，探索并解决下列问题：
1. （1）分解因式：x²﹣6x﹣7；
2. （2）分解因式：a²＋4ab﹣5b²
答案解析收藏纠错 + 选题