
 B .
B .  C .
C .  D .
D . 
 B .
B . 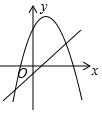 C .
C . 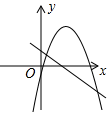 D .
D . 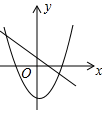

(参考数据: ,
,
,
,
,
)

90,92,93,95,95,96,96,96,97,100.
竞赛成绩分组统计表
组别 | 竞赛成绩分组 | 频数 | 平均分 |
1 | 8 | 65 | |
2 | 75 | ||
3 | 88 | ||
4 | 10 | 95 |
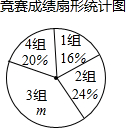
请根据以上信息,解答下列问题:
最长边长为128的整数边三角形有多少个?(整数边三角形是指三边长度都是整数的三角形.)
问题探究:
为了探究规律,我们先从最简单的情形入手,从中找到解决问题的方法,最后得出一般性的结论.
①如表①,最长边长为1的整数边三角形,显然,最短边长是1,第三边长也是1.按照(最长边长,最短边长,第三边长)的形式记为 , 有1个,所以总共有
个整数边三角形.
表①
|
最长边长 |
最短边长 |
(最长边长,最短边长,第三边长) |
整数边三角形个数 |
计算方法 |
算式 |
|
1 |
1 |
|
1 |
1个1 |
|
②如表②,最长边长为2的整数边三角形,最短边长是1或2.根据三角形任意两边之和大于第三边,当最短边长为1时,第三边长只能是2,记为 , 有1个;当最短边长为2时,显然第三边长也是2,记为
, 有1个,所以总共有
个整数边三角形.
表②
|
最长边长 |
最短边长 |
(最长边长,最短边长,第三边长) |
整数边三角形个数 |
计算方法 |
算式 |
|
2 |
1 |
|
1 |
2个1 |
|
|
2 |
|
1 |
③下面在表③中总结最长边长为3的整数边三角形个数情况:
表③
|
最长边长 |
最短边长 |
(最长边长,最短边长,第三边长) |
整数边三角形个数 |
计算方法 |
算式 |
|
3 |
1 |
|
1 |
2个2 |
|
|
2 |
|
2 |
|||
|
3 |
|
1 |
④下面在表④中总结最长边长为4的整数边三角形个数情况:
表④
|
最长边长 |
最短边长 |
(最长边长,最短边长,第三边长) |
整数边三角形个数 |
计算方法 |
算式 |
|
4 |
1 |
|
1 |
3个2 |
|
|
2 |
|
2 |
|||
|
3 |
|
2 |
|||
|
4 |
|
1 |
表⑤
|
最长边长 |
最短边长 |
(最长边长,最短边长,第三边长) |
整数边三角形个数 |
计算方法 |
算式 |
|
5 |
1 |
|
1 |
....... |
....... |
|
2 |
|
2 |
|||
|
3 |
...... |
...... |
|||
|
4 |
|
2 |
|||
|
5 |
|
1 |
最长边长为6的整数边三角形有个.
在直三棱柱中,若所有棱长均为整数,则最长棱长为9的直三棱柱有个.