河南省百校联考2021年中考数学模拟试卷（三）

更新时间：2022-05-05 浏览次数：128 类型：中考模拟

一、单选题

1. (2021·河南模拟) $\text{[math]}$ 的绝对值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·河南模拟) 国资委数据显示，2020年中央企业累计实现营业收入30.3万亿元，累计实现净利润1.4万亿元，同比增长2.1%.近八成中央企业净利润同比正增长.将数据“30.3万亿”用科学记数法可表示为（）

A . 3.03×10¹⁰ B . 30.3×10¹³ C . 3.03×10¹³ D . 3.03×10¹⁴

答案解析收藏纠错 + 选题
3. (2021·河南模拟) 如图是由大小相同的小正方体搭成的几何体的俯视图，小正方形内的数字表示该位置上小正方体的数量.将数字“3”的位置上最上方的一个小正方体向数字“2”的位置上平移，关于平移前后几何体的三视图，下列说法正确的是（）

A . 主视图与左视图改变 B . 左视图与俯视图不变 C . 主视图与俯视图不变 D . 三种视图都不变

答案解析收藏纠错 + 选题
4. (2021·河南模拟) 如图，在△ABC中，点E，F分别在边AC，BC上，EF∥AB.若CE＝2AE，AB＝4，则EF的长为（）

A . $\text{[math]}$ B . 1 C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·河南模拟) 某市为了落实脱贫攻坚战中“两不愁、三保障”的住房保障工作，2018年投入4.5亿元资金，之后投入资金逐年增长，2020年投入6.2亿元资金用于保障性住房建设.设该市这两年投入资金的年平均增长率为x，则可列方程为（）

A . 4.5（1+2x）＝6.2 B . 4.5×2（1+x）＝6.2 C . 6.2（1﹣x）²＝4.5 D . 4.5（1+x）²＝6.2

答案解析收藏纠错 + 选题
6. (2022九下·新会模拟) 一种营养粥是由糯米、黑米和红豆三种主要原料配比后熬制而成，且权重之比为5：4：1.经市场了解发现，糯米、黑米和红豆的价格分别为6元/千克、8元/千克和20元/千克，仅从主要原料角度考虑，这种营养粥的成本价为（）

A . 8.5元/千克 B . 6.8元/千克 C . 7.6元/千克 D . 8.2元/千克

答案解析收藏纠错 + 选题
7. (2021·河南模拟) 若点A（﹣1，y₁），B（2，y₂），C（﹣2，y₃），D（m，﹣m）均在反比例函数y＝ $\text{[math]}$ （k≠0）的图象上，则y₁ ， y₂ ， y₃大小关系是（）

A . y₂＜y₃＜y₁ B . y₃＜y₂＜y₁ C . y₁＜y₃＜y₂ D . y₁＜y₂＜y₃

答案解析收藏纠错 + 选题
8. (2023九上·启东期末) 对于向上抛出的物体，在没有空气阻力的条件下，满足这样的关系式：h＝vt﹣ $\text{[math]}$ gt² ，其中h是上升高度，v是初始速度，g为重力加速度（g≈10m/s²），t为抛出后的时间.若v＝20m/s，则下列说法正确的是（）

A . 当h＝20m时，对应两个不同的时刻点 B . 当h＝25m时，对应一个时刻点 C . 当h＝15m时，对应两个不同的时刻点 D . h取任意值，均对应两个不同的时刻点

答案解析收藏纠错 + 选题
9. (2023·天河模拟) 如图，在▱OABC中，边OC在x轴上，点A（1， $\text{[math]}$ ），点C（3，0）.按以下步骤作图：分别以点B，C为圆心，大于 $\text{[math]}$ BC的长为半径作弧，两弧相交于E，F两点；作直线EF，交AB于点H；连接OH，则OH的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·河南模拟) 如图，在正方形ABCD中，点A（0，2），点B（3，0），点C和点D均在第一象限内，将正方形ABCD绕点O逆时针旋转，每秒旋转60°，则第51秒时点D的坐标为（）

A . （5，﹣2） B . （﹣3，﹣5） C . （﹣3，5） D . （﹣2，﹣5）

答案解析收藏纠错 + 选题

二、填空题

11. (2021·河南模拟) 如图，点A为数轴上一点，对应的实数为a.若﹣a＜b＜a﹣1，请写出一个符合条件的整数b的值.

答案解析收藏纠错 + 选题
12. (2021·河南模拟) 不等式组 $\text{[math]}$ 的整数解为.

答案解析收藏纠错 + 选题
13. (2021·河南模拟) 为了缓解中考备考压力，增加学习兴趣，李老师带领同学们玩转盘游戏.如图为两个转盘，转盘一被四等分，分别写有汉字“中”“考”“必”“胜”；转盘二被三等分，分别写有汉字“我”“必”“胜”.将两个转盘各转动一次（当指针指向区域分界线时，不记，重转），若得到“必”“胜”两字，则获得游戏一等奖，请求出获得游戏一等奖的概率为.

答案解析收藏纠错 + 选题
14. (2024九下·惠阳月考) 如图1，是一枚残缺的古代钱币，如图2，经测量发现，钱币完好部分的弧长为3π，其内部正方形ABCD的边长为1.已知正方形ABCD的中心与⊙O的圆心重合，且点E，F分别是边BC，CD的延长线与⊙O的交点，则图中阴影部分的面积为.

答案解析收藏纠错 + 选题
15. (2021·河南模拟) 如图，在正方形ABCD中，AB＝8，点E，F分别为边AB，AD上的动点，且EF＝6，点G，M分别为边BC，CD的中点，连接BM，DG交于点O.将△EFA沿EF折叠得到△EFA'，点H是边EF上一动点，连接A'H，HO，OA'.当A'H+HO的值最小时，OA'的长为 .

答案解析收藏纠错 + 选题

三、解答题

16. (2021·河南模拟) 下面是小斌同学进行分式化简的过程，请认真阅读并解答问题.
$\text{[math]}$
＝ $\text{[math]}$ …第一步
＝ $\text{[math]}$ …第二步
＝ $\text{[math]}$ …第三步
＝ $\text{[math]}$ …第四步
＝ $\text{[math]}$ …第五步
＝ $\text{[math]}$ …第六步
1. （1）填空：
  a.以上化简步骤中，第步是进行分式的通分，通分的依据是.
  b.第步开始出现错误，这一步错误的原因是①_ ， ②.
2. （2）请直接写出该分式化简后的正确结果.
3. （3）除纠正上述错误外，请你根据平时的学习经验，就分式化简时还需要注意的事项给其他同学提一条建议.
答案解析收藏纠错 + 选题
17. (2021·河南模拟) [收集数据]某数学兴趣小组在甲，乙两个班各随机抽取了18名学生的成绩x（单位：分，满分120分），如表.
甲班
108
112
96
93
109
99
103
97
105
84
78
88
96
72
84
86
98
102
乙班
113
94
111
108
75
86
80
77
74
99
105
100
86
89
76
93
88
84
[整理数据]整理以上数据，得到两个班样本数据的成绩频数分布表.
成绩
频数
班级
72≤x＜84
84≤x＜96
96≤x＜108
108≤x＜120
甲班
2
5
8
3
乙班
5
7
3
3
[分析数据]根据以上数据，得到以下统计量.
统计量
班级
平均数
中位数
众数
优秀率
（分数不低于96分）
甲班
95
a
84，96
m%
乙班
91
88.5
b
33.3%
根据以上信息，回答下列问题：
1. （1）表格中的a＝_ ， b＝_.
2. （2）计算m的值.（结果保留一位小数）
3. （3）在此次抽样调查中，与小明所在的班级相比，小明的成绩高于平均数，却排在了后九名，则小明是_班的学生.
4. （4）结合上表中的统计量，判断哪个班学生的成绩较好，并说明理由.
答案解析收藏纠错 + 选题

18. (2021·河南模拟) 在学完锐角三角函数后，某班利用自制的测角仪和卷尺，测量校国旗杆的高度，他们制定了如下两种测量方案.

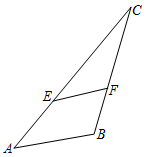
方案一：第一步：在国旗杆前平地上选择一点A作为测量点，用自制的测角仪测出观察者看国旗杆顶端D的仰角α；第二步：在点A和国旗杆底端点C之间选择一点B，测出由点B看国旗顶端D的仰角β；第三步：测出AB两点间的距离；第四步：计算国旗杆的高度CD.

方案二：第一步：在国旗杆前平地上选择一点A，用自制的测角仪测出观察者（竖直站立）看国旗杆顶端D的仰角α；第二步：测量观察者眼睛到地面的竖直高度AE；第三步：测量点A到国旗杆底端C的水平距离AC；第四步：在点A处重复上述操作，得到仰角及距离；第五步：计算国旗杆的高度CD.根据以上方案，测量信息汇总如下：

课题	测量校园旗杆的高度
方案	方案一				方案二
测量示意图
测量数据	测量项目	α	β	AB的长	测量项目		α	AE的长	AC的长
	数据	33°	45°	5.99m	数据	第一次	32.7°	151cm	17.47m
						第二次	33.3°	153cm	17.45m
						平均值	a	152cm	b

（1） ①填空：a＝， b＝；
②请判断哪个方案更好，并说明理由.
（2）根据你的判断，选择合适的数据计算出国旗杆的高度.（结果保留一位小数.参考数据：sin33°≈0.545，cos33°≈0.839，tan33°≈0.649）

答案解析收藏纠错 + 选题

19. (2021·河南模拟) 为了净化空气，美化校园环境，某学校计划种植A，B两种树木.已知购买20棵A种树木和15棵B种树木共花费2680元；购买10棵A种树木和20棵B种树木共花费2240元.
1. （1）求A，B两种树木的单价分别为多少元.
2. （2）如果购买A种树木有优惠，优惠方案是：购买A种树木超过20棵时，超出部分可以享受八折优惠.若该学校购买m（m＞0，且m为整数）棵A种树木花费w元，求w与m之间的函数关系式.
3. （3）在（2）的条件下，该学校决定在A，B两种树木中购买其中一种，且数量超过20棵，请你帮助该学校判断选择购买哪种树木更省钱.
答案解析收藏纠错 + 选题
20. (2021·河南模拟) 某兴趣小组通过探究圆的基本知识，找到了借助圆作“过直线外一点作已知直线的平行线”的方法，如图，过点C作直线l的平行线.作图过程如下：

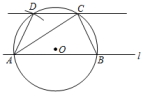
第一步：在直线l上任意取两点A，B，连接AC，BC，且AC＞BC；

第二步：作△ABC的外接圆O；

第三步：以点A为圆心，CB长为半径作弧，交 $\text{[math]}$ 于点D，连接AD；

第四步：作直线CD，则直线CD即为所求作的平行线.
1. （1）为了说明这一方法的正确性，需要对其进行证明如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程.
  已知：如图，△ABC内接于⊙O，AC＞BC，D为弧AC上一点，且满足.求证：.
2. （2）聪聪认为，在△ABC中，若AC＝BC，过点C作直线l的平行线 $\text{[math]}$ ，则 $\text{[math]}$ 为⊙O的切线，你认为聪聪的想法正确吗？请说明理由.
答案解析收藏纠错 + 选题
21. (2021·河南模拟) 如图，抛物线y＝ax²﹣2ax﹣3a（a为常数，且a≠0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，且OC＝OB，D为抛物线的顶点.
1. （1）求抛物线的解析式及顶点D的坐标.
2. （2）点P为抛物线上一动点，过点P作PQ∥AB，交抛物线于点Q.若点C到PQ的距离大于2个单位长度，求点Q的横坐标x₀的取值范围.
答案解析收藏纠错 + 选题

22. (2021·河南模拟) 小明在学习中遇到这样一个问题：

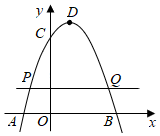
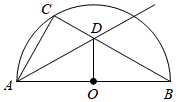
如图，点C是半圆O上一动点（不与点A，B重合），直径AB＝8cm.射线AD平分∠CAB交BC于点D，连接OD.当△AOD为等腰三角形时，求线段AC的长度.

小明同学尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整：

（1）根据点C在半圆O上的不同位置，画出相应的图形，测量线段AC，AD，OD的长度，得到下表的几组对应值.

AC/m	1.0	2.0	3.0	4.0	5.0	6.0	7.0
AD/m	1.32	2.53	3.63	m	5.54	6.41	7.23
OD/m	3.13	2.53	2.25	n	2.60	3.02	3.50

当AC＝4cm时，无需测量，请直接写出m，n的值.（结果保留两位小数.参考数据： $\text{[math]}$ ≈1.732）

（2）设线段AC的长为自变量x，AD的长为函数y₁ ， OD的长为函数y₂ ，在同一平面直角坐标系中描出以上表中各组对应值为坐标的点，如图所示，请描出剩余的点并画出函数y₁ ， y₂的图象.
（3）继续在同一坐标系中画出所需的函数图象，并结合图象直接写出：当△AOD为等腰三角形时，线段AC长度的近似值.（结果保留一位小数）

答案解析收藏纠错 + 选题

23. (2021·河南模拟) 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，CD⊥AB于点D，线段EF在直线BC上（点E在点F的左侧），且EF＝CB，过点F作直线CD的垂线，垂足为G，连接AE，AG，EG.
1. （1）如图1，当点E和点C重合时，△AEG的形状为_ ， $\text{[math]}$ ＝_.
2. （2）如图2，当线段EF在直线BC上移动时，请判断 $\text{[math]}$ 的值是否发生变化.若不变，请仅就图2的情形给出证明；若改变，请说明理由.
3. （3）若AB＝4 $\text{[math]}$ ，当以点A，B，G，F为顶点的四边形为平行四边形时，请直接写出GE的长.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河南省百校联考2021年中考数学模拟试卷（三）

副标题：

*注意事项：

河南省百校联考2021年中考数学模拟试卷（三）

试题分析

总体分析

题量分析

难度分析

知识点分析

甲班	108	112	96	93	109	99	103	97	105
甲班	84	78	88	96	72	84	86	98	102
乙班	113	94	111	108	75	86	80	77	74
乙班	99	105	100	86	89	76	93	88	84