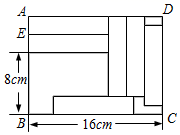
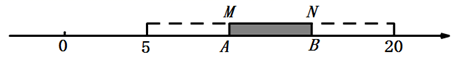
①这列火车长150米;②这列火车的行驶速度为10米每秒;
③若保持原速度不变,则这列火车通过长160米的隧道丙需用时18秒;
④若速度变为原速度的两倍,则这列火车通过隧道甲的时间将变为原来的一半.
①一次性购物不超过100元不享受优惠;
②一次性购物超过100元但不超过300元,一律9折
③一次性购物超过300元,一律8折
小李两次购物分别付款80元,252元,如果他一次性购买以上两次相同的商品,应付款
|
工艺 |
每天可加工药材的吨数 |
出品率 |
售价(元/吨) |
|
粗加工 |
14 |
80% |
5000 |
|
精加工 |
6 |
60% |
11000 |
注:①出品率本指加工后所得产品的质量与原料的重量的比值,②加工后的废品不产生效益,
受市场影响,请公司必须在10天内将这批药材加工完毕,现有3种方案:
A.全部粗加工,则获利多少元?
B尽可能多的精加工,剩余的直接在市场上销售,则可获利多少元;
C部分粗加工,部分精加工,恰好10天完成,可获利多少元?
问:哪个方案获得的利润最大?是多少?
|
甲 |
乙 |
|
|
修建速度(米/天) |
90 |
80 |
|
每天所需工程费(元) |
1200 |
1000 |
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
![]()
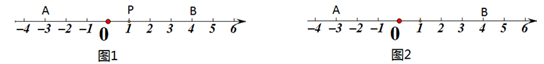
填空:①若点P表示的数为-2,则n的值为;
②数轴上表示整数的点称为整点,若整点P为A、B的“7节点”,则这样的整点P共有个.
![]()
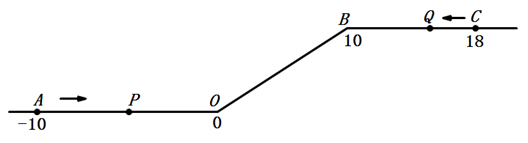
①当P运动到C点时,点Q所表示的数是多少?
②当t为何值时,P、Q之间的距离为6?
③若点P与点C之间的距离表示为PC,点Q与点B之间的距离表示为QB.在运动过程中,是否存在某一时刻使得PC + QB = 5?若存在,请求出此时点P表示的数;若不存在,请说明理由.
射线 是
内部的一条射线,若
,则我们称射线
是射线
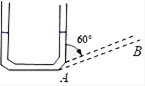
的伴随线.如图1,
,
,则
,称射线
是射线
的伴随线;同时,由于
,称射线
是射线
的伴随线.
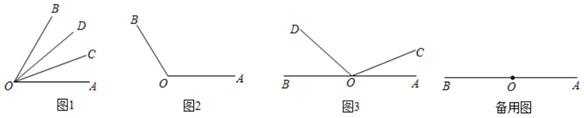
如图2, ,射线
是射线
的伴随线,则
.若
的度数是
,射线
是射线
的伴随线,则
的度数是.(用含
的代数式表示).
①是否存在某个时刻 (秒),使得
的度数是
,若存在,求出
的值,若不存在,请说明理由.
②当 为多少秒时,射线
、
、
中恰好有一条射线是其余两条射线中某一条射线的伴随线,请直接写出
的值.