东北三省三校2022届高三理数第二次联合模拟考试试卷

更新时间：2022-04-25 浏览次数：98 类型：高考模拟

一、单选题

1. (2022·东北模拟) 设 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·东北模拟) 复数 $\text{[math]}$ （其中i为虚数单位）的模为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
3. (2022·东北模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 9 B . 24 C . 27 D . 33

答案解析收藏纠错 + 选题
4. (2022·东北模拟) 命题“ $\text{[math]}$ ， $\text{[math]}$ ”的否定是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·东北模拟) 为研究变量x，y的相关关系，收集得到下面五个样本点（x，y）：
x
9
9.5
10
10.5
11
y
11
10
8
6
5
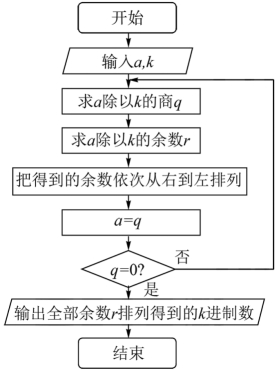
若由最小二乘法求得y关于x的回归直线方程为 $\text{[math]}$ ，则据此计算残差为0的样本点是（）

A . （9，11） B . （10，8） C . （10.5，6） D . （11.5）

答案解析收藏纠错 + 选题
6. (2022·东北模拟) 将函数 $\text{[math]}$ 图象上各点的横坐标伸长为原来的2倍，再向右平移 $\text{[math]}$ 个单位，所得图象对应的函数（）

A . 在区间 $\text{[math]}$ 上单调递增 B . 在区间（ $\text{[math]}$ ， $\text{[math]}$ ）上单调递减 C . 图象关于点（ $\text{[math]}$ ， 0）对称 D . 图象关于直线 $\text{[math]}$ 对称

答案解析收藏纠错 + 选题
7. (2022·东北模拟) 盒子中装有编号为0，1，2，3，4，5，6的7个球，从中任意取出两个，则这两个球的编号之和为3的倍数的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·东北模拟) 已知圆锥的顶点为点S，底面圆心为点O，高是底面半径r的 $\text{[math]}$ 倍，点A，B是底面圆周上的两点，若△SAB是等边三角形，则O到平面SAB的距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·东北模拟) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·东北模拟) 定义域为R的奇函数 $\text{[math]}$ 满足 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 0

答案解析收藏纠错 + 选题
11. (2022·东北模拟) 已知实数 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2022·东北模拟) 我们常说函数 $\text{[math]}$ 的图象是双曲线，建立适当的平面直角坐标系，可求得这个双曲线的标准方程为 $\text{[math]}$ ．函数 $\text{[math]}$ 的图象也是双曲线，在适当的平面直角坐标系中，它的标准方程可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2022·东北模拟) 在爱尔兰小说《格列佛游记》里，有格列佛在小人国一顿吃了1728份小人饭的叙述，作者为什么要使用这么复杂的数字呢？许多研究者认为，之所以选用这个数字，跟英国人计数经常使用的十二进制有关系．中国文化中，十二进制也有着广泛应用，如12地支，12个时辰，12生肖…．十二进制数通常使用数字0—9以及字母A，B表示，其中A即数字10，B即数字11．对于下面的程序框图，若输入a=1728，k=12，则输出的数为．

答案解析收藏纠错 + 选题
14. (2022·东北模拟) 在正六边形 $\text{[math]}$ 中，点 $\text{[math]}$ 为线段 $\text{[math]}$ （含端点）上的动点，若 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ），则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
15. (2022·东北模拟) 椭圆C： $\text{[math]}$ （ $\text{[math]}$ ）的左焦点为点F，过原点O的直线与椭圆交于P，Q两点，若∠PFQ=120°， $\text{[math]}$ ， $\text{[math]}$ ，则椭圆C的离心率为．

答案解析收藏纠错 + 选题
16. (2022高二上·辽宁期中) 如图，多面体ABCDEF中，面ABCD为正方形，DE⊥平面ABCD，CF∥DE，且AB=DE=2，CF=1，G为棱BC的中点，H为棱DE上的动点，有下列结论：
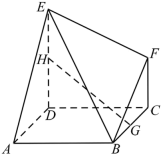
①当H为DE的中点时，GH∥平面ABE；
②存在点H，使得GH⊥AE；
③三棱锥B−GHF的体积为定值；
④三棱锥E−BCF的外接球的表面积为 $\text{[math]}$ ．
其中正确的结论序号为．（填写所有正确结论的序号）

答案解析收藏纠错 + 选题

三、解答题

17. (2022·东北模拟) 如图，正三棱柱 $\text{[math]}$ 中， $\text{[math]}$ ，点D是棱 $\text{[math]}$ 的中点．
1. （1）求证： $\text{[math]}$ ；
2. （2）求二面角 $\text{[math]}$ 的余弦值．
答案解析收藏纠错 + 选题
18. (2022·东北模拟) 近期，国家出台了减轻义务教育阶段学生作业负担和校外培训负担“双减”政策．为了坚决落实“双减”政策，提高教学质量，提升课后服务水平，某中心小学计划实行课后看护工作．现随机抽取该中心小学三年级的10个班级并调查了解需要课后看护的学生人数，如下面频数分布表：
班级代号
1
2
3
4
5
6
7
8
9
10
需看护学生人数
20
18
27
30
24
23
32
35
21
20
已知该中心小学每个班级50人，为了节约资源并保证每个看护教室有两名看护教师，该校计划：若需要课后看护的学生人数超过25人的班级配备1名班主任和1名其他科任教师；若需要课后看护的学生人数不超过25人的班级只配备1名班主任，但需要和另一个人数不超过25人的班级合班看护．
1. （1）若将上述表格中人数不超过25人的6个班两两组合进行课后看护，求班级代号为1，2的两个班合班看护的概率；
2. （2）从已抽取的10个班级中随机抽取3个班，记3个班中需要课后看护的学生人数超过25人的班级数为X，求X的分布列及数学期望．
答案解析收藏纠错 + 选题
19. (2022·东北模拟) 已知等差数列 $\text{[math]}$ 公差不为零， $\text{[math]}$ ， $\text{[math]}$ ，数列 $\text{[math]}$ 各项均为正数， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求数列 $\text{[math]}$ ， $\text{[math]}$ 的通项公式；
2. （2）若 $\text{[math]}$ 恒成立，求实数 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
20. (2024高二下·江门月考) 已知函数 $\text{[math]}$ （ $\text{[math]}$ ， e为自然对数的底数）．
1. （1）若 $\text{[math]}$ 在x=0处的切线与直线y=ax垂直，求a的值；
2. （2）讨论函数 $\text{[math]}$ 的单调性；
3. （3）当 $\text{[math]}$ 时，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2023·铜川模拟) 已知点F为抛物线E： $\text{[math]}$ （ $\text{[math]}$ ）的焦点，点P（−3，2）， $\text{[math]}$ ，若过点P作直线与抛物线E顺次交于A，B两点，过点A作斜率为1的直线与抛物线的另一个交点为点C．
1. （1）求抛物线E的标准方程；
2. （2）求证：直线BC过定点；
3. （3）若直线BC所过定点为点Q，△QAB，△PBC的面积分别为S₁ ， S₂ ，求 $\text{[math]}$ 的取值范围
答案解析收藏纠错 + 选题
22. (2022·东北模拟) 在平面直角坐标系 $\text{[math]}$ 中，以原点为极点， $\text{[math]}$ 轴正半轴为极轴建立极坐标系，点 $\text{[math]}$ 的极坐标分别为 $\text{[math]}$ ，圆 $\text{[math]}$ 以 $\text{[math]}$ 为直径，直线 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$ ．
1. （1）求圆 $\text{[math]}$ 及直线 $\text{[math]}$ 的直角坐标方程；
2. （2）圆 $\text{[math]}$ 经过伸缩变换 $\text{[math]}$ 得到曲线 $\text{[math]}$ ，已知点 $\text{[math]}$ 为曲线 $\text{[math]}$ 上的任意一点，求点 $\text{[math]}$ 到直线 $\text{[math]}$ 距离的取值范围．
答案解析收藏纠错 + 选题
23. (2022·东北模拟) 已知函数 $\text{[math]}$ 的值域为 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题