2022年浙教版数学九上复习阶梯训练：第1章二次函数（优...

更新时间：2022-05-12 浏览次数：70 类型：复习试卷

一、单选题

1. 如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（

A . y= $\text{[math]}$ B . y= $\text{[math]}$ C . y= $\text{[math]}$ D . y= $\text{[math]}$

答案解析收藏纠错 + 选题
2. 已知菱形ABCD的边长为1，∠DAB=60°，E为AD上的动点，F在CD上，且AE+CF=1，设ΔBEF的面积为y，AE=x，当点E运动时，能正确描述y与x关系的图像是：（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021九上·上思期中) 如图所示，已知二次函数y=ax²+bx+c的图象与x轴交于A、B两点，与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax²+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：
①2a+b+c＞0；②a﹣b+c＜0；③x（ax+b）≤a+b；④a＜﹣1.

其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
4. (2021九上·诸暨月考) 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，对称轴为直线x＝﹣1，下列结论不正确的是（）

A . b²＞4ac B . abc＞0 C . a﹣c＜0 D . am²+bm≥a﹣b（m为为任意实数）

答案解析收藏纠错 + 选题
5. (2021九上·怀宁期末) 已知二次函数y＝ax²+bx+c与自变量x的部分对应值如表，下列说法不正确的是（）
x
…
﹣1
0
1
3
…
y
…
﹣3
1
3
1
…

A . a＜0 B . 方程ax²+bx+c＝﹣2的正根在4与5之间 C . 2a+b＞0 D . 若点（5，y₁）、（﹣ $\text{[math]}$ ， y₂）都在函数图象上，则y₁＜y₂

答案解析收藏纠错 + 选题
6. (2021九上·温州期末) 二次函数 $\text{[math]}$ 的部分图象如图所示，当 $\text{[math]}$ 时，函数值 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021九上·瑶海月考) 如图，是二次函数y=ax²+bx+c（a≠0）的图象的一部分，给出下列命题：
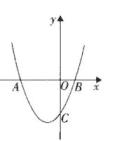
①abc＜0；②b＞2a；③a+b+c=0；④8a+c＞0；⑤ax²+bx+c=0的两根分别为﹣3和1．

其中正确的命题有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
8. (2021九上·朝阳期末) 将抛物线 $\text{[math]}$ 在x轴上方的部分记为 $\text{[math]}$ ，在x轴上及其下方的部分记为 $\text{[math]}$ ，将 $\text{[math]}$ 沿x轴向下翻折得到 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 两部分组成的图象记为M．若直线 $\text{[math]}$ 与M恰有2个交点，则m的取值范围为（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·朝阳期中) 将二次函数y＝﹣x²+2x+3的图象在x轴上方的部分沿x轴翻折后，所得新函数的图象如图所示.当直线y＝x+b与新函数的图象恰有3个公共点时，b的值为（）

A . $\text{[math]}$ 或﹣3 B . $\text{[math]}$ 或﹣3 C . $\text{[math]}$ 或﹣3 D . $\text{[math]}$ 或﹣3

答案解析收藏纠错 + 选题
10. (2021九上·上城期中) 已知抛物线y＝﹣x²+bx+c与x轴交于点A（m﹣2，0）和B（2m+1，0）（点A在点B的左侧），对称轴为l：x＝1，直线y＝kx+2（k≠0）与抛物线相交于两点M（x₁ ， y₁），N（x₂ ， y₂）（x₁＜x₂），则|x₁﹣x₂|最小值为（）

A . 4 B . 4 $\text{[math]}$ C . 2 D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2022·安徽模拟) 已知抛物线y=-x²+bx+c（b、c为常数）．
1. （1）当c=-4时，抛物线与x轴有且只有一个交点，则b=；
2. （2）当c=2b²时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最大值为18，则b的值．
答案解析收藏纠错 + 选题
12. (2022九下·长兴月考) 如图是王明正在设计的一动画示意图，×轴上依次有A，B，C三个点，且AB=2，在BC上方有五个台阶（各拐角均为90°），每个台阶的高、宽分别是1和1.5，第一个台阶到x轴距离BD=10．从点A处向右，上方沿抛物线y=-x²+4x+12发出一个带光的点P．当点P落在台阶上时，落点的坐标是．

答案解析收藏纠错 + 选题
13. (2021九上·龙凤期末) 我们定义一种新函数：形如y＝|ax²+bx+c|（a≠0，且b²﹣4ac＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y＝|x²﹣2x﹣3|的图像（如图所示），并写出下列结论：
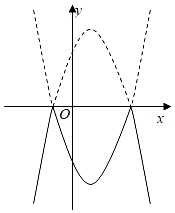
①图像与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；
②图像具有对称性，对称轴是直线x＝1；
③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；
④当x＝﹣1或x＝3时，函数的最小值是0；
⑤当x＝1时，函数的最大值是4；
⑥若点P（a，b）在该图像上，则当b＝2时，可以找到4个不同的点P．其中错误的结论是（填序号）．

答案解析收藏纠错 + 选题
14. (2021九上·北流期中) 如图，已知二次函数 $\text{[math]}$ （a≠0（的图象，且关于x的一元二次方程 $\text{[math]}$ 没有实数根，有下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ .其中正确结论的序号有.

答案解析收藏纠错 + 选题
15. (2022九上·福州开学考) 如图，正方形ABCD的边长为2，E为边AD上一动点，连接CE，以CE为边向右侧作正方形CEFG，连接DF，DG，则 $\text{[math]}$ 面积的最小值为．

答案解析收藏纠错 + 选题
16. (2019九上·滨湖期末) 记抛物线C₁：y＝(x﹣2)²+3的顶点为A，抛物线C₂：y＝ax²+1(a＜0)顶点是点B，且与x轴的正半轴交于点 C.当△ABC是直角三角形时，抛物线C₂的解析式为.

答案解析收藏纠错 + 选题

三、综合题

17. (2022·东昌府模拟) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与x轴，y轴相交于A，B两点，点C的坐标是 $\text{[math]}$ ．连接AC，BC．
1. （1）求过O，A，C三点的抛物线的函数表达式，并判断△ABC的形状；
2. （2）动点P从点O出发，沿OB以每秒2个单位长度的速度向点B运动；同时，动点Q从点B出发，沿BC以每秒1个单位长度的速度向点C运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为ts，当t为何值时， $\text{[math]}$ BPQ的面积最大？
3. （3）当抛物线的对称轴上有一点M，使以A，B，M为顶点的三角形是等腰三角形时，求出点M的坐标．
答案解析收藏纠错 + 选题
18. (2022·周村模拟) 抛物线 $\text{[math]}$ 过点A(-1，0)，B(3，0)，与y轴交于点C．对称轴与x轴交于点D．
1. （1）求抛物线的解析式及点D的坐标：
2. （2）如图，连接CD、CB，在直线BC上方的抛物线上找点P，使得 $\text{[math]}$ ，求出P点的坐标：
3. （3）点M为直线BC上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以C，D，M，N为顶点的四边形是菱形？若存在，求出点M的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
19. (2022·瑶海模拟) 已知：抛物线y＝－x²＋kx＋k＋1（k＞1）与x轴交于A、B两点，（点A在点B的左侧），与y轴交于点C．
1. （1） k＝2时，求抛物线的顶点坐标；
2. （2）若抛物线经过一个定点，求这个定点的坐标；
3. （3）点P为抛物线上一点，且位于直线BC上方，过点P作PF∥y轴，交BC于点F，求PF长度的最大值（用含k式子表示）．
答案解析收藏纠错 + 选题
20. (2022·安庆模拟) 已知函数 $\text{[math]}$ （m为常数），问：
1. （1）无论m取何值，该函数的图象总经过x轴上某一定点，该定点坐标为；
2. （2）求证：无论m为何值，该函数的图象顶点都在函数 $\text{[math]}$ 图像上：
3. （3）若抛物线 $\text{[math]}$ 与x轴有两个交点A、B，且 $\text{[math]}$ ，求线段AB的最大值．
答案解析收藏纠错 + 选题
21. (2022·) 某童装店销售某款童装，每件售价为60元，每星期可卖100件，为了促销，该店决定降价销售，经市场调查反应：每降价2元，每星期可多卖20件．已知该款童装每件成本为40元．设该款童装每件售价为x元，销售量为y件．
1. （1）每星期的销售量y =(用含x的代数式表示y并化简)；
2. （2）当每件童装售价定为多少元时，该店一星期可获得2210元的利润？
3. （3）当每件售价定为多少元时，每星期的销售利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
22. (2022九下·泾阳月考) 如图，二次函数y=ax²+bx-3的图象与x轴交于A（-3，0），B（1，0）两点，与y轴交于点C．
1. （1）求该二次函数的表达式；
2. （2）若点D在x轴的上方，以A、B、D为顶点的三角形与△ABC全等，平移该二次函数图象，使平移后的图象经过点B与点D，请你写出平移过程，并说明理由．
答案解析收藏纠错 + 选题
23. (2022九上·长沙月考) 我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于直线 $\text{[math]}$ （n为常数）对称，则把该函数称之为“ $\text{[math]}$ 函数”.
1. （1）在下列关于x的函数中，是“ $\text{[math]}$ 函数”的是（填序号）；
  ① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$
2. （2）若关于x的函数 $\text{[math]}$ （h为常数）是“ $\text{[math]}$ 函数”，与 $\text{[math]}$ （m为常数， $\text{[math]}$ ）相交于A（ $\text{[math]}$ ， $\text{[math]}$ ）、B（ $\text{[math]}$ ， $\text{[math]}$ ）两点，A在B的左边， $\text{[math]}$ ，求m的值；
3. （3）若关于x的“ $\text{[math]}$ 函数” $\text{[math]}$ （a，b为常数）经过点（ $\text{[math]}$ ，1），且 $\text{[math]}$ ，当 $\text{[math]}$ 时，函数的最大值为 $\text{[math]}$ ，最小值为 $\text{[math]}$ ，且 $\text{[math]}$ ，求t的值.
答案解析收藏纠错 + 选题
24. (2022九下·重庆开学考) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点（点A在点B的左侧），与y轴交于点C，连接AC、BC，点P为直线BC上方抛物线上一动点，连接OP交BC于点Q.
1. （1）求抛物线的函数表达式；
2. （2）当 $\text{[math]}$ 的值最大时，求点P的坐标和 $\text{[math]}$ 的最大值；
3. （3）把抛物线 $\text{[math]}$ 沿射线AC方向平移 $\text{[math]}$ 个单位得新抛物线 $\text{[math]}$ ，M是新抛物线上一点，N是新抛物线对称轴上一点，当以M、N、B、C为顶点的四边形是平行四边形时，直接写出N点的坐标，并把求其中一个N点坐标的过程写出来.
答案解析收藏纠错 + 选题
25. (2022九下·重庆开学考) 如图1，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，交y轴于点 $\text{[math]}$
1. （1）求抛物线的解析式；
2. （2）如图2，点P为直线AC上方且抛物线对称轴左侧的抛物线上一点，过点P作х轴的平行线交抛物线于点D，过点P作y轴的平行线交AC于点H，求 $\text{[math]}$ 的最大值及此时点P的坐标；
3. （3）把抛物线 $\text{[math]}$ 向右平移 $\text{[math]}$ 个单位，再向上平移 $\text{[math]}$ 个单位得新抛物线，在新抛物线对称轴上找一点M，在新抛物线上找一点N，直接写出所有使得以点A，C，M，N为顶点的四边形是平行四边形的点M的坐标，并把求其中一个点M的坐标的过程写出来.
答案解析收藏纠错 + 选题