河南省信阳市2022年中考数学一模试卷

更新时间：2022-06-13 浏览次数：87 类型：中考模拟

一、单选题

1. (2024七上·乌鲁木齐月考) 下列各数： $\text{[math]}$ ， $\text{[math]}$ ， 0， $\text{[math]}$ ，其中比 $\text{[math]}$ 小的数是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·信阳模拟) 如图，将一个圆柱体放置在长方体上，其中圆柱体的底面直径与长方体的宽相平，则该几何体的左视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023九下·阳朔模拟) 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作，根据规划“一带一路”地区覆盖总人口为 $\text{[math]}$ 人， $\text{[math]}$ 的原数是（）

A . 440000000 B . 44000000000 C . 440000000000 D . 4400000000

答案解析收藏纠错 + 选题
4. (2023九上·道外期中) 下列运算一定正确的是（）

A . a²+a²＝a⁴ B . a²•a⁴＝a⁸ C . （a²）⁴＝a⁸ D . （a+b）²＝a²+b²

答案解析收藏纠错 + 选题
5. (2022·信阳模拟) 如图，已知直线AD、BE、CF相交于点O，OG⊥AD，且∠BOC=35°，∠FOG=30°，则∠DOE的度数为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·信阳模拟) 下列关于 $\text{[math]}$ 的一元二次方程中，有两个不相等的实数根的方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·信阳模拟) 在4张完全相同的卡片上分别标上2，3，4，5这四个数字，任意抽取两张卡片并将所标数字组成一个两位数，则这个两位数能被3整除的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·信阳模拟) 如图，点A在双曲线y═ $\text{[math]}$ （x＞0）上，过点A作AB⊥x轴，垂足为点B，分别以点O和点A为圆心，大于 $\text{[math]}$ OA的长为半径作弧，两弧相交于D，E两点，作直线DE交x轴于点C，交y轴于点F（0，2），连接AC．若AC=1，则k的值为（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·信阳模拟) 如图，平面直角坐标系中，A（4，0），点B为y轴上一点，连接AB，tan∠BAO＝2，点C，D为OB，AB的中点，点E为射线CD上一个动点、当△AEB为直角三角形时，点E的坐标为（　　）

A . （4，4）或（2 $\text{[math]}$ 2，4） B . （4，4）或（2 $\text{[math]}$ 2，4） C . （12，4）或（2 $\text{[math]}$ 2，4） D . （12，4）或（2 $\text{[math]}$ 2，4）

答案解析收藏纠错 + 选题
10. (2022·信阳模拟) 如图1，一个扇形纸片的圆心角为90°，半径为6．如图2，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD ，图中阴影为重合部分，则阴影部分的面积为（）

A . 6π﹣ $\text{[math]}$ B . 6π﹣9 $\text{[math]}$ C . 12π﹣ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2022·信阳模拟) 比较大小：2 $\text{[math]}$ 5.（选填“＞”“＜”或“＝”）

答案解析收藏纠错 + 选题
12. (2022·信阳模拟) 如图，直线AB与直线CD相交于点O，点E是∠COB内一点，且OE⊥AB，∠AOC＝35°，则∠EOD的度数是.

答案解析收藏纠错 + 选题
13. (2022·信阳模拟) 如图所示的网格中，每个小正方形的边长为1，点A，B，C均为小正方形的顶点，且点B在 $\text{[math]}$ 上，则阴影部分的面积为.

答案解析收藏纠错 + 选题
14. (2022·信阳模拟) 如图1，在平面直角坐标系中，直线y $\text{[math]}$ x+m（m＞0）与直线y＝2x交于点4，与x轴交于点B，点O为坐标原点，点C在线段OB上，且不与点B重合，过点C作垂直于x轴的直线，交直线AB于点D，将△BCD沿CD翻折，得到△ECD.设点C的坐标为（x，0），△CDE与△AOB重叠部分的面积为S，S关于x的函数图象如图2所示，则m＝.

答案解析收藏纠错 + 选题
15. (2022·信阳模拟)

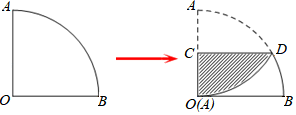
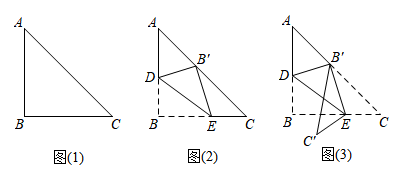
如图（1），在等腰直角三角形纸片ABC中，∠B＝90°，AB＝2 $\text{[math]}$ 2，点D，E分别为AB，BC上的动点.将纸片沿DE翻折，点B的对应点B'恰好落在边AC上，如图（2），再将纸片沿B'E翻折，点C的对应点为C'，如图（3）.当△DB'E，△B'C'E的重合部分（即阴影部分）为直角三角形时，CE的长为.

答案解析收藏纠错 + 选题

三、解答题

16. (2022·信阳模拟)
1. （1）计算：|﹣4|﹣（ $\text{[math]}$ ）^﹣² $\text{[math]}$ tan30°+ $\text{[math]}$ .
2. （2）化简： $\text{[math]}$ .
答案解析收藏纠错 + 选题

17. (2022·信阳模拟) 地铁为我们提供了方便、舒适、快捷的出行条件，但地铁上也有一些不文明的现象.某市记者为了解“乘坐地铁时的不文明行为”，随机调查了该市部分市民，并对调查结果进行整理，绘制了如下尚不完整的统计图表.

组别	观点	频数（人数）
A	破坏先下后上的规矩堵进出口	80
B	占座	m
C	拒绝安检	n
D	吃东西、随手丢垃圾	120
E	其他	60

请根据图表中提供的信息解答下列问题.

（1）填空：m=，n=，扇形统计图中E组所占的百分比为%.
（2）若从这次接受调查的市民中随机抽出一人，则此人持C组观点的概率是多少？
（3）若该市约有100万人，请你估计其中持D组观点的人数.

答案解析收藏纠错 + 选题

18. (2022·信阳模拟) 如图，在△ABC中，AB＝AC＝6cm，∠BAC＝45°，以AB为直径作⊙O，分别与AC，BC相交于点E，D，连接DE，BE，点F从点A出发，在直径AB的上方沿 $\text{[math]}$ 以1cm/s的速度向点B运动，连接AF，BF.设点F运动的时间为t（s）.
1. （1）求证：△ABC∽△DEC；
2. （2）填空：①当t＝　　s时，四边形AEBF为正方形.
  ②当t＝　　s时，S△ABF $\text{[math]}$ S△AB_E.
答案解析收藏纠错 + 选题
19. (2022·信阳模拟) 如图，在矩形OABC中，BC＝4，OC，OA分别在x轴、y轴上，对角线OB，AC交于点E；过点E作EF⊥OB，交x轴于点F.反比例函数 $\text{[math]}$ （x＞0）的图象经过点E，且交BC于点D，已知S△OEF＝5，CD＝1.
1. （1）求OF的长；
2. （2）求反比例函数的解析式；
3. （3）将△OEF沿射线EB向右上方平移 $\text{[math]}$ 个单位长度，得到△O'E'F'，则EF的对应线段E'F'的中点（填“能”或“不能”）落在反比例函数 $\text{[math]}$ （x＞0）的图上.
答案解析收藏纠错 + 选题
20. (2022·信阳模拟) 如图（1）为某大型商场的自动扶梯，图（2）中的AB为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点A处时，测得天花板上日光灯C的仰角为37°，此时他的眼睛D与地面的距离AD＝1.8m，之后他沿一楼扶梯到达顶端B后又沿BL（BL∥MN）向正前方走了2m，发现日光灯C刚好在他的正上方.已知自动扶梯AB的坡度为1：2.4，AB的长度是13m，求日光灯C到一楼地面的高度.（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

答案解析收藏纠错 + 选题
21. (2022·信阳模拟) 为美化校园，某校需补栽甲、乙两种花苗.经咨询，这两种花苗的价格都有零售价和批发价之分（若按批发价购买，则每种花苗购买数量不少于100株），零售时每株甲种花苗比每株乙种花苗多5元.已知用零售价购买相同数量的甲、乙两种花苗，所用费用分别是100元、50元.
1. （1）求甲、乙两种花苗的零售价；
2. （2）该校预计批发这两种花苗共1000株，且甲种花苗的数量不少于乙种花苗数量的 $\text{[math]}$ ，甲、乙两种花苗的批发价分别为8元/株、2元/株.设甲种花苗的批发数量为m株，相比按零售价购买可节约的资金总额为W元，求W与m之间的函数关系式，并求节约资金总额的最大值.
答案解析收藏纠错 + 选题
22. (2022·信阳模拟) 如图，抛物线y＝ax²+3x+c与x轴交于点A，B，直线y＝x+1与抛物线交于点A，C（3，n）.点P为抛物线上一动点，其横坐标为m.
1. （1）求抛物线的解析式及其顶点的坐标；
2. （2）已知直线l：x＝m+5与直线AC交于点D，过点P作PE⊥l于点E，以PE，DE为边作矩形PEDF.
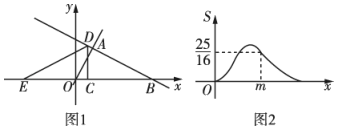
  ①当抛物线的顶点在矩形PEDF内部时，请直接写出m的取值范围.
  ②在①的条件下，求矩形PEDF的周长的最小值.
答案解析收藏纠错 + 选题
23. (2022·信阳模拟) 在△ABC中，AB＝AC，∠BAC＝90°，点D，E分别是AC，BC的中点，点P是直线DE上一点，连接AP，将线段PA绕点P顺时针旋转90°得到线段PM，连接AM，CM.
1. （1）问题发现
  如图（1），当点P与点D重合时，线段CM与PE的数量关系是，∠ACM＝°.
2. （2）探究证明
  当点P在射线ED上运动时（不与点E重合），（1）中结论是否一定成立？请仅就图中的情形给出证明.
3. （3）问题解决
  连接PC，当△PCM是等边三角形时，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题