 B .
B .  C .
C .  D .
D . 

① ,②方程
的两个根是
,
,③
,④当
时,x的取值范围是
.

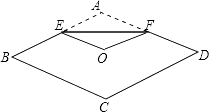
①作 的角平分线交
于点E;
②作线段 的垂直平分线交
于点F.
八年级抽取的学生的竞赛成绩:
4,10,8,6,6,6,7,7,7,6,9,9,8,8,8,8,8,9,10,4.
|
七年级抽取的学生的竞赛成绩条形统计图
|
七、八年级抽取的学生的竞赛成绩统计表
|
根据以上信息,解答下列问题:
|
目的地车型 |
A地(元/辆) |
B地(元/辆) |
|
大货车 |
900 |
1000 |
|
小货车 |
500 |
700 |
现安排上述装好物资的20辆货车中的10辆前往A地,其余前往B地,设前往A地的大货车有x辆,这20辆货车的总运费为y元.
①写出S与t之间的函数关系式,并写出t的取值范围;
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?若存在,请求出R点的坐标;若不存在,请说明理由.