 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人 数 | 4 | 8 | 12 | 11 | 5 |
则该办学生成绩的众数和中位数分别是( )
 B .
B .  C .
C . 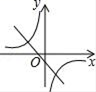 D .
D . 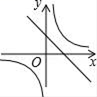
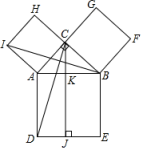
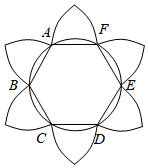
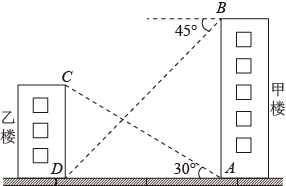
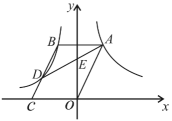

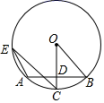
①已知直线AB与y轴交于A点,与轴交于B点,sin∠ABO=
, OB=4,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;
②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=25上的一点,若△APD是以D为直角顶点的等腰直角三角形,请求出所有符合条件的点D的坐标.
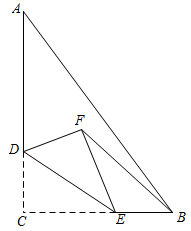
①如图1,过点 作
轴于点
,作
轴于点
,当
时,求
的长;

②如图2,该抛物线上是否存在点 ,使得
?若存在,请求出所有点
的坐标;若不存在,请说明理由.
