四川省广元市苍溪县2020-2021学年八年级下学期期末数学...

更新时间：2024-07-13 浏览次数：57 类型：期末考试

一、单选题

1. (2024八下·红花岗期中) 下列各式中，运算正确的是（）

A . $\text{[math]}$ ＝﹣2 B . $\text{[math]}$ + $\text{[math]}$ ＝ $\text{[math]}$ C . $\text{[math]}$ × $\text{[math]}$ ＝4 D . 2﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022八下·汶上月考) 下列四组线段中，能组成直角三角形的是（　　）.

A . a=1，b=2，c=3 B . a=2，b=3，c=4 C . a=2，b=4，c=5 D . a=3，b=4，c=5

答案解析收藏纠错 + 选题
3. (2023八下·盘山期末) 函数y=2x﹣5的图象经过（）

A . 第一、三、四象限 B . 第一、二、四象限 C . 第二、三、四象限 D . 第一、二、三象限

答案解析收藏纠错 + 选题
4. (2021八下·苍溪期末) 某市一周日最高气温如图所示，则该市这周的日最高气温的众数是（）

A . 25 B . 26 C . 27 D . 28

答案解析收藏纠错 + 选题
5. (2021八下·苍溪期末) 要得到函数y=2x+3的图象，只需将函数y=2x的图象（）

A . 向左平移3个单位 B . 向右平移3个单位 C . 向下平移3个单位 D . 向上平移3个单位

答案解析收藏纠错 + 选题
6. (2021八下·苍溪期末) 如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2，则AC的长为（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
7. (2022八下·鄂伦春期末) 已知P₁（﹣3，y₁），P₂（2，y₂）是一次函数y=﹣x﹣1的图象上的两个点，则y₁ ， y₂的大小关系是（）

A . y₁=y₂ B . y₁＜y₂ C . y₁_＞y₂ D . 不能确定

答案解析收藏纠错 + 选题
8. (2021八下·苍溪期末) 一家公司打算招聘一名翻译对甲、乙、丙三名应试者进行了听、说、读、写的英语水平测试，他们各项成绩（百分制）如下表所示：
应试者
听
说
读
写
甲
73
80
82
83
乙
85
78
85
73
丙
80
82
80
80
如果这家公司想招一名笔译能力较强的翻译，听、说、读、写成绩按照2：1：3：4的比确定，从他们的平均成绩（百分制）看，应该录取（）

A . 甲 B . 乙 C . 丙 D . 不确定

答案解析收藏纠错 + 选题
9. (2023七下·蚌埠期末) 如图，已知：函数y＝3x+b和y＝ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式3x+b＞ax﹣3的解集是（）

A . x＞﹣5 B . x＞﹣2 C . x＞﹣3 D . x＜﹣2

答案解析收藏纠错 + 选题
10. (2021八下·苍溪期末) 设max表示两个数中的最大值，例如： $\text{[math]}$ ， $\text{[math]}$ ，则关于 $\text{[math]}$ 的函数 $\text{[math]}$ 可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023八下·大兴期中) 若 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
12. (2023八下·石屏期末) 已知一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的平均数是2，那么另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2的平均数是．

答案解析收藏纠错 + 选题
13. (2024九上·简阳月考) 计算 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
14. (2021八下·苍溪期末)
如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为

答案解析收藏纠错 + 选题
15. (2022八下·潮安期末) 如图，点A在线段BG上，四边形ABCD和四边形DEFG都是正方形，面积分别是10和19，则△CDE的面积为.

答案解析收藏纠错 + 选题
16. (2021八下·苍溪期末) 一次函数y₁＝kx+b与y₂＝x+a的图象如图，则下列结论：①k $\text{[math]}$ 0；②a $\text{[math]}$ 0；③关于x的方程kx﹣x＝a﹣b的解是x＝3；④当x $\text{[math]}$ 3时，y₁ $\text{[math]}$ y₂中．则正确的序号有．

答案解析收藏纠错 + 选题

三、解答题

17. (2021八下·苍溪期末) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021八下·苍溪期末) 小明根据学习函数的经验，对函数y＝﹣|x|+3的图象与性质进行了探究.下面是小明的探究过程，请你解决相关问题.
1. （1）如表y与x的几组对应值：
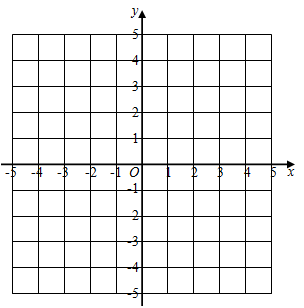
  x
  …
  ﹣4
  ﹣3
  ﹣2
  ﹣1
  0
  1
  2
  3
  4
  …
  y
  …
  ﹣1
  0
  1
  2
  3
  2
  1
  a
  ﹣1
  …
  ①a＝；
  ②若A（b，﹣7），B（10，﹣7）为该函数图象上不同的两点，则b＝；
2. （2）如图，在平面直角坐标系中，描出以上表中各对对应值为坐标的点，并根据描出的点，画出该函数的图象：
  ①该函数有 ▲ （填“最大值”或“最小值”）；并写出这个值为 ▲ ；
  ②求出函数图象与坐标轴在第二象限内所围成的图形的面积；
  ③观察函数y＝﹣|x|+3的图象，写出该图象的两条性质.
答案解析收藏纠错 + 选题
19. (2020七上·蓬莱期末) 如图所示的一块地，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求这块地的面积.

答案解析收藏纠错 + 选题
20. (2021八下·苍溪期末) 如图，在▱ABCD中，E是AD的中点，延长CB到点F，使 $\text{[math]}$ ，连接BE、AF.
1. （1）完成画图并证明四边形AFBE是平行四边形；
2. （2）若AB=6，AD=8，∠C=60°，求BE的长.
答案解析收藏纠错 + 选题

21. (2022八下·侯马期末) 我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

（1）根据图示填写下表；

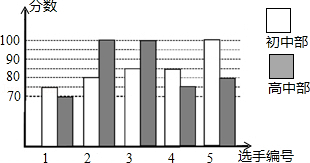
	平均数（分）	中位数（分）	众数（分）
初中部		85
高中部	85		100

（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.

答案解析收藏纠错 + 选题

22. (2021八下·苍溪期末) 如图，在平行四边形ABCD中，点E是边BC的中点，连接AE并延长，交DC的延长线于点F，连接AC，BF.
1. （1）求证：△ABE≌△FCE；
2. （2）当四边形ABFC是矩形时，若∠AEC＝120°，求∠D的度数.
答案解析收藏纠错 + 选题
23. (2021八下·苍溪期末) 如图，一次函数y＝ax+b的图象与正比例函数y＝kx的图象交于点M ，
1. （1）求正比例函数和一次函数的解析式；
2. （2）根据图象写出使正比例函数的值大于一次函数的值的x的取值范围；
3. （3）求△MOP的面积．
答案解析收藏纠错 + 选题
24. (2021八下·苍溪期末) 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．
1. （1）求证：四边形OCED是菱形；
2. （2）若∠BAC=30°，AC=4，求菱形OCED的面积．
答案解析收藏纠错 + 选题
25. (2021八下·苍溪期末) 学校计划从某苗木基地购进A、B两咱树苗共200棵绿化校园.已知购买了3棵A种树苗和5棵B种树苗共需700元；购买2棵A种树苗和1棵B种树苗共需280元.
1. （1）每棵A种树苗、B种树苗各需多少元？
2. （2）学校除支付购买树苗的费用外，平均每棵树苗还需支付运输及种植费用20元.设学校购买B种树苗x棵，购买两种树苗及运输、种植所需的总费用为y元，求y与x的函数关系；
3. （3）在（2）的条件下，若学校用于绿化的总费用在22400元限额内，且购买A种树苗的数量不少于B种树苗的数量，请给出一种费用最省的方案，并求出该方案所需的费用.
答案解析收藏纠错 + 选题
26. (2021八下·苍溪期末) 已知：甲乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．
1. （1）求甲车离出发地的距离y_甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
2. （2）它们出发 $\text{[math]}$ 小时时，离各自出发地的距离相等，求乙车离出发地的距离y_乙（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
3. （3）在（2）的条件下，求它们在行驶的过程中相遇的时间．
答案解析收藏纠错 + 选题