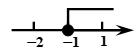
 D .
D . 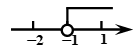


|
小惠: 证明:∵AC⊥BD,OB=OD, ∴AC垂直平分BD. ∴AB=AD,CB=CD, ∴四边形ABCD是菱形. |
小洁: 这个题目还缺少条件,需要补充一个条件才能证明. |
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
①当a=1时,152=225=1×2×100+25;
②当a=2时,252=625=2×3×100+25;
③当a=3时,352=1225=;
……
|
x(h) |
… |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
… |
|
Y(cm |
… |
189 |
137 |
103 |
80 |
101 |
133 |
202 |
260 |
… |
(数据来自某海洋研究所)
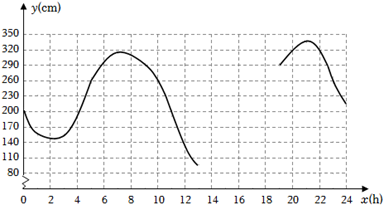
①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
请结合函数图象,写出该函数的两条性质或结论.
根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?

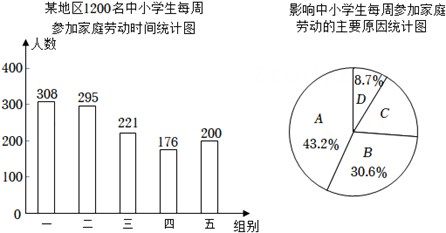
中小学生每周参加家庭劳动时间x(h)分为5组:第一组(0≤x<0.5),第二组(0.5≤x<1),第三组(1≤x<1.5),第四组(1.5≤x<2),第五组(x≥2).
根据以上信息,解答下列问题:
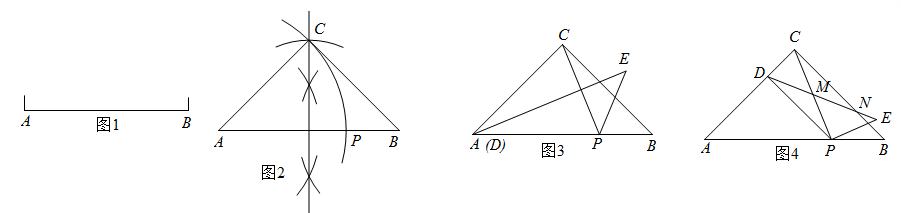
①如图3,当点D运动到点A时,求∠CPE的度数.
②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.