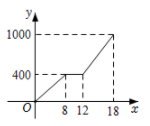
 B .
B . 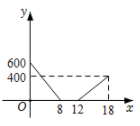 C .
C . 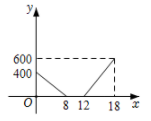 D .
D . 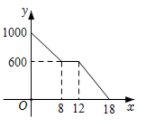

|
x(b) |
…… |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
…… |
|
y(cm) |
…… |
189 |
137 |
103 |
80 |
101 |
133 |
202 |
260 |
…… |
(数据来自某海举研究所)
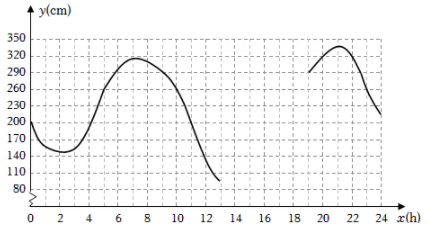
①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
请结合函数图象,写出该函数的两条性质或结论.
根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?