内蒙古赤峰市松山区2022届高三理数第三次统一模拟考试试卷

更新时间：2024-07-13 浏览次数：103 类型：高考模拟

一、单选题

1. (2022·松山模拟) 已知集合 $\text{[math]}$ 的所有非空真子集的元素之和等于12，则 $\text{[math]}$ 的值为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
2. (2022·松山模拟) 若复数z满足 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ 是纯虚数 C . 复数z在复平面内对应的点在第三象限 D . 若复数z在复平面内对应的点在角α的终边上，则 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·松山模拟) 下列函数中，既是奇函数又在定义域内递增的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·松山模拟) 若x，y满足约束条件 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . -1 B . -2 C . 0 D . 2

答案解析收藏纠错 + 选题
5. (2022·松山模拟) 直线 $\text{[math]}$ 的倾斜角为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·松山模拟) 我国南宋著名数学家秦九韶提出了由三角形三边求三角形面积的“三斜求积”公式，设 $\text{[math]}$ 的三个内角A，B，C所对的边分别为a，b，c，面积为S，“三斜求积”公式表示为 $\text{[math]}$ .在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，则用“三斜求积”公式求得 $\text{[math]}$ 的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·松山模拟) 甲、乙两名学生的六次数学测验成绩(百分制)的茎叶图如图所示.
①甲同学成绩的中位数大于乙同学成绩的中位数；②甲同学的平均分比乙同学的平均分高；③甲同学的平均分比乙同学的平均分低；④甲同学成绩的方差小于乙同学成绩的方差.以上说法正确的是（）

A . ③④ B . ①② C . ②④ D . ①③④

答案解析收藏纠错 + 选题
8. (2022高二上·大荔期末) 从某个角度观察篮球(如图1)，可以得到一个对称的平面图形，如图2所示，篮球的外轮形为圆O ，将篮球表面的粘合线看成坐标轴和双曲线，若坐标轴和双曲线与圆O的交点将圆O的周长八等分，AB＝BC＝CD ，则该双曲线的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·松山模拟) 下列函数中，最小值为9的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·松山模拟) 椭圆 $\text{[math]}$ 的左右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ， O为坐标原点，给出以下四个命题：
①过点 $\text{[math]}$ 的直线与椭圆C交于A，B两点，则 $\text{[math]}$ 的周长为8；②椭圆C上存在点P，使得 $\text{[math]}$ ；③椭圆C的离心率为 $\text{[math]}$ ；④P为椭圆 $\text{[math]}$ 一点，Q为圆 $\text{[math]}$ 上一点，则点P，Q的最大距离为3.
则以下选项正确的是（）

A . ①② B . ①③ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
11. (2022·松山模拟) 已知函数 $\text{[math]}$ ，若 $\text{[math]}$ ，则有（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2022·松山模拟) 若干个正方体形状的积木按下图所示摆成塔型：上方正方体中下底面的四个顶点是下面相邻正方体中上底面各边的中点，最下面的正方体的棱长为1，平放于桌面上，如果所有正方体能直接看到的表面积超过8.8，则正方体的个数至少是（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题

二、填空题

13. (2022·松山模拟) 锅中煮有芝麻馅汤圆6个，花生馅汤圆5个，豆沙馅汤圆4个，这三种汤圆的外部特征完全相同.从中任意舀取4个汤圆，则每种汤圆都至少取到1个的概率为.（用分数作答）

答案解析收藏纠错 + 选题
14. (2022·松山模拟) 如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积为.

答案解析收藏纠错 + 选题
15. (2022·松山模拟) 如图，某中学校园中央有一座钟楼，某学生为了测量钟楼高AB，该学生先在钟楼的正西方点C处测得钟楼顶部的仰角为45°，然后从点C处沿南偏东30°方向前进60 $\text{[math]}$ 到达点D处，在D处测得钟楼顶部的仰角为30°，则钟楼AB的高度是 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2022·松山模拟) 数学美的表现形式不同于自然美或艺术美那样直观，它蕴藏于抽象的概念、公式、符号、推理论证、思维方法等之中，是一种科学的真实美．平面直角坐标系中，曲线 $\text{[math]}$ 就是一条形状优美的曲线，对于此曲线，给出如下结论：
①曲线 $\text{[math]}$ 围成的图形的面积是 $\text{[math]}$ ；
②曲线 $\text{[math]}$ 上的任意两点间的距离不超过 $\text{[math]}$ ；
③若 $\text{[math]}$ 是曲线 $\text{[math]}$ 上任意一点，则 $\text{[math]}$ 的最小值是 $\text{[math]}$ ．
其中正确的有（填上所有正确结论的序号）．

答案解析收藏纠错 + 选题

三、解答题

17. (2022·松山模拟) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）记 $\text{[math]}$ ，写出 $\text{[math]}$ ，并求数列 $\text{[math]}$ 的通项公式；
2. （2）求 $\text{[math]}$ 的前20项和.
答案解析收藏纠错 + 选题
18. (2022·松山模拟) 两会期间国家对学生学业与未来发展以及身体素质的重要性的阐述引起了全社会的共鸣.某中学体育组对高三的800名男生做了单次引体向上的测试，得到了如图所示的频率分布直方图（引体向上个数只记整数）.体育组为进一步了解情况，组织了两个研究小组.
1. （1）第一小组决定从单次完成1-15个引体向上的男生中，按照分层抽样抽取22人进行全面的体能测试.
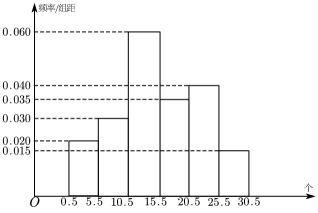
  ①在单次完成6-10个引体向上的所有男生中，男生甲被抽到的概率是多少？
  ②该小组又从这22人中抽取3人进行个别访谈，记抽到“单次完成引体向上1-5个”的人数为随机变量X，求X的分布列和数学期望；
2. （2）第二小组从学校学生的成绩与体育锻炼相关性角度进行研究，得到了这800人的学业成绩与体育成绩之间的 $\text{[math]}$ 列联表.
  
  学业优秀
  学业不优秀
  总计
  体育成绩不优秀
  200
  400
  600
  体育成绩优秀
  100
  100
  200
  总计
  300
  500
  800
  请你根据列联表判断是否有99.5%的把握认为体育锻炼与学业成绩有关？
  参考公式：独立性检验统计量 $\text{[math]}$ ，其中 $\text{[math]}$ .
  下面的临界值表供参考：
  $\text{[math]}$
  0.15
  0.10
  0.05
  0.025
  0.010
  0.005
  0.001
  $\text{[math]}$
  2.072
  2.706
  3.841
  5.024
  6.635
  7.879
  10.828
答案解析收藏纠错 + 选题
19. (2022·松山模拟) 如图，在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ 底面ABCD， $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）试在棱PC上找一点E满足： $\text{[math]}$ ；
2. （2）若F为棱PC上一点，满足 $\text{[math]}$ ，求二面角 $\text{[math]}$ 的余弦值.
答案解析收藏纠错 + 选题
20. (2022·松山模拟) 已知抛物线 $\text{[math]}$ 的准线经过点 $\text{[math]}$ ，过点 $\text{[math]}$ 的直线l与抛物线C有两个不同的交点A，B，点 $\text{[math]}$ （其中 $\text{[math]}$ ）在抛物线C上，且直线PA交y轴于M，直线PB交y轴于N.
1. （1）求直线l斜率的取值范围；
2. （2）设O为原点，若 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ 为定值.
答案解析收藏纠错 + 选题
21. (2022·松山模拟) 已知函数 $\text{[math]}$ ， $\text{[math]}$
1. （1）证明：当 $\text{[math]}$ 时， $\text{[math]}$ ；
2. （2）试讨论函数 $\text{[math]}$ 在 $\text{[math]}$ 上的零点个数.
答案解析收藏纠错 + 选题
22. (2022·松山模拟) 在直角坐标系xOy中，曲线C₁： $\text{[math]}$ (α为参数)．以原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C₂：ρ²＝4ρcos θ－3.
1. （1）求C₁的普通方程和C₂的直角坐标方程；
2. （2）若曲线C₁与C₂交于A，B两点，A，B的中点为M，点P(0，－1)，求|PM|·|AB|的值．
答案解析收藏纠错 + 选题
23. (2022·松山模拟) 已知函数f（x）＝|x+1|+|x+a|．
（Ⅰ）当a＝﹣1时，求不等式f（x）＞2x的解集；
（Ⅱ）当不等式f（x）＞1的解集为R时，求实数a的取值范围．

答案解析收藏纠错 + 选题