

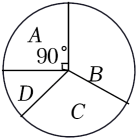
请根据图表中提供的信息,解答下面的问题:
|
人员 |
领队 |
心理医生 |
专业医生 |
专业护士 |
|
占总人数的百分比 |
4% |
|
56% |
|
则该批医护工作人员中“专业医生”占总人数的百分比为.
|
成绩x/分 |
频数 |
频率 |
|
|
15 |
0.1 |
|
|
a |
0.2 |
|
|
45 |
b |
|
|
60 |
c |
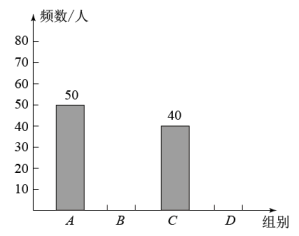
等级 | 成绩x/分 | 人数 |
A | 90≤x≤100 | 15 |
B | 80≤x<90 | a |
C | 70≤x<80 | 18 |
D | x<70 | 7 |

分析数据:
平均数 | 中位数 | 众数 | |
甲组 | a | 80 | 80 |
乙组 | 83 | b | c |
根据以上信息回答下列问题:
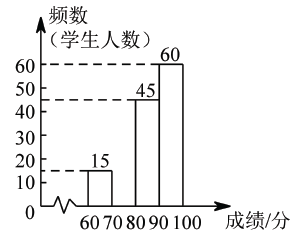
参赛成绩 | ||||
人数 | 8 | 32 | ||
级别 | 及格 | 中等 | 良好 | 优秀 |

请根据所给的信息解答下列问题:
组别 | 锻炼时间(分钟) | 频数(人) | 百分比 |
A |
| 50 | 25% |
B | m | 40% | |
C | 40 | p | |
D | n | 15% |
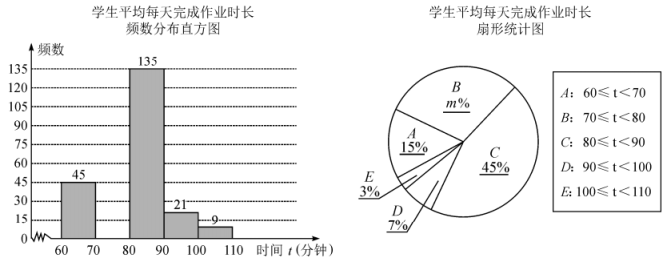
A组: B组:
C组: D组:
E组:
根据调查结果绘制成两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
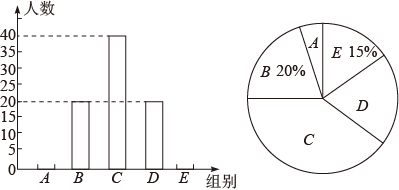
平均每天阅读时间统计表
等级 | 人数(频数) |
A(10≤m<20) | 5 |
B(20≤m<30) | 10 |
C(30≤m<40) | x |
D(40≤m<50) | 80 |
E(50≤m≤60) | y |

请根据图表中的信息,解答下列问题: