甘肃省武威2022年中考数学试卷

更新时间：2024-07-13 浏览次数：247 类型：中考真卷

一、选择题：本大题共10小题，每小题3分，共30分.

1. (2022·孝义模拟) -2的相反数为（）

A . -2 B . 2 C . ±2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·武威) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的余角的大小是（）

A . 50° B . 60° C . 140° D . 160°

答案解析收藏纠错 + 选题
3. (2023·凉州模拟) 不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·石家庄月考) 用配方法解方程x²-2x=2时，配方后正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·武威) 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·武威) 2022年4月16日，神舟十三号载人飞船返回舱在东风着陆场成功着陆，飞行任务取得圆满成功.“出差”太空半年的神舟十三号航天员乘组顺利完成既定全部任务，并解锁了多个“首次”.其中，航天员们在轨驻留期间共完成37项空间科学实验，如图是完成各领域科学实验项数的扇形统计图，下列说法错误的是（）

A . 完成航天医学领域实验项数最多 B . 完成空间应用领域实验有5项 C . 完成人因工程技术实验项数比空间应用领域实验项数多 D . 完成人因工程技术实验项数占空间科学实验总项数的24.3%

答案解析收藏纠错 + 选题
7. (2022·武威) 大自然中有许多小动物都是“小数学家”，如图1，蜜蜂的蜂巢结构非常精巧、实用而且节省材料，多名学者通过观测研究发现：蜂巢巢房的横截面大都是正六边形.如图2，一个巢房的横截面为正六边形 $\text{[math]}$ ，若对角线 $\text{[math]}$ 的长约为8mm，则正六边形 $\text{[math]}$ 的边长为（）

A . 2mm B . $\text{[math]}$ C . $\text{[math]}$ D . 4mm

答案解析收藏纠错 + 选题
8. (2024九下·深圳模拟) 《九章算术》是中国古代的一部数学专著，其中记载了一道有趣的题：“今有凫起南海，七日至北海；雁起北海，九日至南海.今凫雁俱起，问何日相逢？”大意是：今有野鸭从南海起飞，7天到北海；大雁从北海起飞，9天到南海.现野鸭从南海、大雁从北海同时起飞，问经过多少天相遇？设经过x天相遇，根据题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·武威) 如图，一条公路（公路的宽度忽略不计）的转弯处是一段圆弧（ $\text{[math]}$ ），点 $\text{[math]}$ 是这段弧所在圆的圆心，半径 $\text{[math]}$ ，圆心角 $\text{[math]}$ ，则这段弯路（ $\text{[math]}$ ）的长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·武威) 如图1，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿折线 $\text{[math]}$ 方向匀速运动，运动到点 $\text{[math]}$ 停止.设点 $\text{[math]}$ 的运动路程为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的函数图象如图2所示，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本大题共8小题，每小题3分，共24分.

11. (2024八下·东坡月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2024九下·长沙模拟) 因式分解 $\text{[math]}$ = ．

答案解析收藏纠错 + 选题
13. 若一次函数y=kx−2的函数值y随着自变量x值的增大而增大，则k=（写出一个满足条件的值）.

答案解析收藏纠错 + 选题
14. (2024八下·吉林月考) 如图，菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为cm.

答案解析收藏纠错 + 选题
15. (2021九上·丰县期中) 如图，在⊙O内接四边形 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，在不添加任何辅助线的前提下，要想四边形 $\text{[math]}$ 成为一个矩形，只需添加的一个条件是.

答案解析收藏纠错 + 选题
17. (2022九上·天津期中) 如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线.若不考虑空气阻力，小球的飞行高度 $\text{[math]}$ （单位：m）与飞行时间 $\text{[math]}$ （单位：s）之间具有函数关系： $\text{[math]}$ ，则当小球飞行高度达到最高时，飞行时间 $\text{[math]}$ s.

答案解析收藏纠错 + 选题
18. (2022·武威) 如图，在矩形ABCD中，AB=6cm，BC=9cm，点E，F分别在边AB，BC上，AE=2cm，BD，EF交于点G，若G是EF的中点，则BG的长为cm.

答案解析收藏纠错 + 选题

三、解答题：本大题共5小题，共26分.解答时，应写出必要的文字说明、证明过程或演算步骤.

19. (2023七下·桥西期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. (2024九下·庄浪期中) 化简： $\text{[math]}$ .

答案解析收藏纠错 + 选题

21. (2022·武威) 中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编（图1），书中记载了大量几何作图题，所有内容均用浅近的文言文表述，第一编记载了这样一道几何作图题：

原文

释义

甲乙丙为定直角.

以乙为圆心，以任何半径作丁戊弧；

以丁为圆心，以乙丁为半径画弧得交点己；

再以戊为圆心，仍以原半径画弧得交点庚；

乙与己及庚相连作线.

如图2， $\text{[math]}$ 为直角.

以点 $\text{[math]}$ 为圆心，以任意长为半径画弧，交射线 $\text{[math]}$ ， $\text{[math]}$ 分别于点 $\text{[math]}$ ， $\text{[math]}$ ；

以点 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 长为半径画弧与 $\text{[math]}$ 交于点 $\text{[math]}$ ；

再以点 $\text{[math]}$ 为圆心，仍以 $\text{[math]}$ 长为半径画弧与 $\text{[math]}$ 交于点 $\text{[math]}$ ；

作射线 $\text{[math]}$ ， $\text{[math]}$ .

（1）根据以上信息，请你用不带刻度的直尺和圆规，在图2中完成这道作图题（保留作图痕迹，不写作法）；
（2）根据（1）完成的图，直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系.

答案解析收藏纠错 + 选题

22. (2022·武威) 灞陵桥位于甘肃省渭源县城南清源河（渭河上游）上，始建于明洪武初年，因“渭水绕长安，绕灞陵，为玉石栏杆灞陵桥”之语，得名灞陵桥（图1），该桥为全国独一无二的纯木质叠梁拱桥.某综合实践研究小组开展了测量汛期某天“灞陵桥拱梁顶部到水面的距离”的实践活动，过程如下：
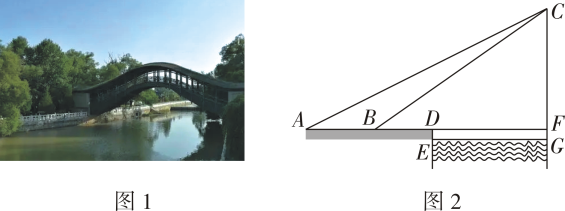
方案设计：如图2，点C为桥拱梁顶部（最高点），在地面上选取A，B两处分别测得∠CAF和∠CBF的度数（A，B，D，F在同一条直线上），河边D处测得地面AD到水面EG的距离DE（C，F，G在同一条直线上，DF∥EG，CG⊥AF，FG=DE）.

数据收集：实地测量地面上A，B两点的距离为8.8m，地面到水面的距离DE=1.5m，∠CAF=26.6°，∠CBF=35°.

问题解决：求灞陵桥拱梁顶部C到水面的距离CG（结果保留一位小数）.

参考数据：sin26 6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50，sin35°≈0.57，cos35°≈0.82，tan35°≈0.70.

根据上述方案及数据，请你完成求解过程.

答案解析收藏纠错 + 选题
23. (2023·会宁模拟) 第24届冬季奥林匹克运动会于2022年2月4至20日在我国北京-张家口成功举办，其中张家口赛区设有四个冬奥会竞赛场馆，分别为：A.云顶滑雪公园、B.国家跳台滑雪中心、C.国家越野滑雪中心、D.国家冬季两项中心.小明和小颖都是志愿者，他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同.
1. （1）小明被分配到D.国家冬季两项中心场馆做志愿者的概率是多少？
2. （2）利用画树状图或列表的方法，求小明和小颖被分配到同一场馆做志愿者的概率.
答案解析收藏纠错 + 选题

四、解答题：本大题共5小题，共40分.解答时，应写出必要的文字说明、证明过程或演算步骤.

24. (2022·武威) 受疫情影响，某初中学校进行在线教学的同时，要求学生积极参与“增强免疫力、丰富学习生活”为主题的居家体育锻炼活动，并实施锻炼时间目标管理.为确定一个合理的学生居家锻炼时间的完成目标，学校随机抽取了30名学生周累计居家锻炼时间（单位：h）的数据作为一个样本，并对这些数据进行了收集、整理和分析，过程如下：
【数据收集】

7 8 6 5 9 10 4 6 7 5 11 12 8 7 6

4 6 3 6 8 9 10 10 13 6 7 8 3 5 10

【数据整理】

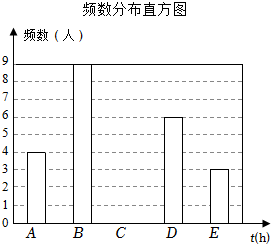
将收集的30个数据按A，B，C，D，E五组进行整理统计，并绘制了如图所示的不完整的频数分布直方图（说明：A. $\text{[math]}$ ，B. $\text{[math]}$ ，C. $\text{[math]}$ ，D. $\text{[math]}$ ，E. $\text{[math]}$ ，其中 $\text{[math]}$ 表示锻炼时间）；

【数据分析】

统计量

平均数

众数

中位数

锻炼时间（h）

7.3

$\text{[math]}$

7

根据以上信息解答下列问题：
1. （1）填空： $\text{[math]}$ ；
2. （2）补全频数分布直方图；
3. （3）如果学校将管理目标确定为每周不少于7h，该校有600名学生，那么估计有多少名学生能完成目标？你认为这个目标合理吗？说明理由.
答案解析收藏纠错 + 选题
25. (2024·澄海模拟) 如图，B，C是反比例函数y= $\text{[math]}$ （k≠0）在第一象限图象上的点，过点B的直线y=x-1与x轴交于点A，CD⊥x轴，垂足为D，CD与AB交于点E，OA=AD，CD=3.
1. （1）求此反比例函数的表达式；
2. （2）求△BCE的面积.
答案解析收藏纠错 + 选题
26. (2023·平阴模拟) 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
27. (2022·武威) 已知正方形 $\text{[math]}$ ， $\text{[math]}$ 为对角线 $\text{[math]}$ 上一点.
1. （1）【建立模型】如图1，连接 $\text{[math]}$ ， $\text{[math]}$ .求证： $\text{[math]}$ ；
2. （2）【模型应用】如图2， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ .
  ①判断 $\text{[math]}$ 的形状并说明理由；
  
  ②若 $\text{[math]}$ 为 $\text{[math]}$ 的中点，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
3. （3）【模型迁移】如图3， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ .求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
28. (2022·武威) 如图1，在平面直角坐标系中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是线段 $\text{[math]}$ ， $\text{[math]}$ 上的动点（点 $\text{[math]}$ ， $\text{[math]}$ 不与点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 重合）.
1. （1）求此抛物线的表达式；
2. （2）连接 $\text{[math]}$ 并延长交抛物线于点 $\text{[math]}$ ，当 $\text{[math]}$ 轴，且 $\text{[math]}$ 时，求 $\text{[math]}$ 的长；
3. （3）连接 $\text{[math]}$ .
  ①如图2，将 $\text{[math]}$ 沿 $\text{[math]}$ 轴翻折得到 $\text{[math]}$ ，当点 $\text{[math]}$ 在抛物线上时，求点 $\text{[math]}$ 的坐标；
  
  ②如图3，连接 $\text{[math]}$ ，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题