江西省萍乡市2022年九年级第二次学业水平检测（二模）数学试...

更新时间：2022-07-28 浏览次数：59 类型：中考模拟

一、单选题

1. (2022·萍乡模拟) 19的相反数是（）

A . -19 B . $\text{[math]}$ C . $\text{[math]}$ D . 19

答案解析收藏纠错 + 选题
2. (2022·萍乡模拟) 如图所示方式，把图1中正方体的一个角切割掉，形成了如图2的几何体，则如图2的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·萍乡模拟) 下列各式计算正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·萍乡模拟) 对于一列数据(数据个数不少于6），如果去掉一个最大值和一个最小值，那么这列数据分析一定不受影响的是（　　）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
5. (2022·萍乡模拟) 将如图图案剪成若干小块，再分别平移后能够得到①，②，③中的（）

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题
6. (2022·萍乡模拟) 在平面直角坐标系中，若点 $\text{[math]}$ 的横坐标和纵坐标相等，则称点 $\text{[math]}$ 为完美点 $\text{[math]}$ 已知二次函数 $\text{[math]}$ 的图象上有且只有一个完美点 $\text{[math]}$ ，且当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ ，最大值为 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. (2023·永吉模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
8. (2022·萍乡模拟) 今年国庆期间上演的《长津湖》倍受广大观众喜爱，票房一路攀升，上映一周票房就高达326000000元.其中326000000用科学记数法表示为.

答案解析收藏纠错 + 选题
9. (2024九下·秦淮期中) 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重．问：每只雀、燕的重量各为多少？设一只雀的重量为 $\text{[math]}$ 斤，一只燕的重量为 $\text{[math]}$ 斤，则可列方程为．

答案解析收藏纠错 + 选题
10. (2022·萍乡模拟) 设 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
11. (2022·萍乡模拟) 如图，四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，对角线BD恰好平分 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2022·萍乡模拟) 如图，在△ABC 中，AB＝BC＝2，AO＝BO，P 是射线 CO 上的一个动点，∠AOC＝60°，则当△PAB为直角三角形时，AP 的长为.

答案解析收藏纠错 + 选题

三、解答题

13. (2022·萍乡模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2022·萍乡模拟) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，接 $\text{[math]}$ ，E，F，M分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ .求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2022·萍乡模拟) 解不等式组 $\text{[math]}$ ，并把不等式组的解集在数轴上表示出来．

答案解析收藏纠错 + 选题
16. (2022·萍乡模拟) 如图，菱形ABCD及点P ，请仅用无刻度的直尺按要求完成下列作图.
1. （1）如图1，若点P在AB上，请在CD上作出点Q ，使CQ=AP；
2. （2）如图2，若点P在菱形ABCD外，请在菱形外作点Q ，使△CQD≌△APB.
答案解析收藏纠错 + 选题
17. (2022·萍乡模拟) 《小猪佩奇》这部动画片，估计同学们都非常喜欢．周末，小猪佩奇一家4口人（小猪佩奇，小猪乔治，小猪妈妈，小猪爸爸）到一家餐厅就餐，包厢有一圆桌，旁边有四个座位（ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）．
1. （1）小猪佩奇随机坐到 $\text{[math]}$ 座位的概率是；
2. （2）若现在由小猪佩奇，小猪乔治两人先后选座位，用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率．
答案解析收藏纠错 + 选题
18. (2022·萍乡模拟) 如图，双曲线 $\text{[math]}$ 经过 $\text{[math]}$ 斜边的中点 $\text{[math]}$ ，交直角边 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ．
1. （1）求直线 $\text{[math]}$ 的解析式；
2. （2）求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题

19. (2022·萍乡模拟) 为了增强学生的疫情防控意识，响应“停课不停学”号召，某校组织了一次“疫情防控知识”专题网上学习，并进行了一次全校2500名学生都参加的网上测试．阅卷后，教务处随机抽取了100份答卷进行分析统计，发现考试成绩（ $\text{[math]}$ 分）的最低分为51分，最高分为满分100分，并绘制了如下不完整的统计图表．请根据图表提供的信息，解答下列问题：

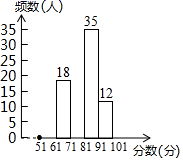
分数段（分）	频数（人）	频率
$\text{[math]}$	$\text{[math]}$	0.1
$\text{[math]}$	18	0.18
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	35	0.35
$\text{[math]}$	12	0.12
合计	100	1

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
（2）将频数分布直方图补充完整；
（3）该校对成绩为 $\text{[math]}$ 的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为 $\text{[math]}$ ，请你估算全校获得二等奖的学生人数；
（4）结合调查的情况，为了提高疫情防控意识，请你给学校提一条合理性建议．

答案解析收藏纠错 + 选题

20. (2024九上·六安月考) 张老师家的洗手盆上装有一种抬启式水龙头（如图①），完全开启后，把手 $\text{[math]}$ 与水平线的夹角为 $\text{[math]}$ ，此时把手端点A、出水口点B和落水点C在同一直线上．洗手盆及水龙头示意图如图②，其相关数据为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求 $\text{[math]}$ 的长（结果精确到 $\text{[math]}$ ．参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）．

答案解析收藏纠错 + 选题
21. (2022·萍乡模拟) 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为直径，过点O作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点F，交 $\text{[math]}$ 于点D，E为 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，其中 $\text{[math]}$ .
1. （1）求证：E是 $\text{[math]}$ 的中点；
2. （2）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
3. （3）如果 $\text{[math]}$ ， $\text{[math]}$ ，求弦 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题

22. (2022·萍乡模拟) 在“新冠病毒”防控期间，某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售，两次购进同一商品的进价相同，具体情况如下表所示：

项目	购进数量（件）		购进所需费用（元）
项目	酒精消毒液	测温枪	购进所需费用（元）
第一次	30	40	8300
第二次	40	30	6400

（1）求酒精消毒液和测温枪两种商品每件的进价分别是多少元？
（2）公司决定酒精消毒液以每件20元出售，测温枪以每件240元出售．为满足市场需求，需购进这两种商品共1000件，且酒精消毒液的数量不少于测温枪数量的4倍，求该公司销售完上述1000件商品获得的最大利润．

答案解析收藏纠错 + 选题

23. (2022·萍乡模拟) 已知：在Rt△ABC中，∠B=90°，∠ACB=30°，点D为BC边上一动点，以AD为边，在AD的右侧作等边三角形ADE．
1. （1）当AD平分∠BAC时，如图1，四边形ADCE是形；
2. （2）过E作EF⊥AC于F，如图2，求证：F为AC的中点；
3. （3）若AB=2，
  ①当D为BC的中点时，过点E作EG⊥BC于G，如图3，求EG的长；
  ②点D从B点运动到C点，则点E所经过路径长为 ▲ ． (直接写出结果)
答案解析收藏纠错 + 选题
24. (2022·萍乡模拟) 在平面直角坐标系中，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ （点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧）两点．点 $\text{[math]}$ 是该抛物线上任意一点，过 $\text{[math]}$ 点作平行于 $\text{[math]}$ 轴的直线交 $\text{[math]}$ 于 $\text{[math]}$ ，分别过点 $\text{[math]}$ ， $\text{[math]}$ 作直线 $\text{[math]}$ 的垂线，垂足分别为点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）已知： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
  ①如图①，当点 $\text{[math]}$ 的横坐标为1，直线 $\text{[math]}$ 轴且过抛物线与 $\text{[math]}$ 轴的交点时， $\text{[math]}$ ， $\text{[math]}$ ；
  ②如图②，当点 $\text{[math]}$ 的横坐标为2，直线 $\text{[math]}$ 的解析式为 $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ．
2. （2）由（1）中两种情况的结果，请你猜想在一般情况下 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并证明你的猜想．
3. （3）若 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 的横坐标分别为-4，2，点 $\text{[math]}$ 在直线 $\text{[math]}$ 的上方的抛物线上运动（点 $\text{[math]}$ 不与点 $\text{[math]}$ ， $\text{[math]}$ 重合），在点 $\text{[math]}$ 的运动过程中，利用（2）中的结论求出 $\text{[math]}$ 的最大面积．
答案解析收藏纠错 + 选题