江苏省无锡市惠山区2021-2022学年七年级下学期期中数学...

更新时间：2022-08-17 浏览次数：89 类型：期中考试

一、单选题

1. (2022七下·惠山期中) 下列运算正确的是（）

A . a＋2a＝3a² B . a³·a²＝a⁵ C . (a⁴)²＝a⁶ D . a³＋a⁴＝a⁷

答案解析收藏纠错 + 选题
2. (2022七下·惠山期中) 新冠病毒（2019－nCoV）是一种新型病毒，它的直径约60～220nm，平均直径为100nm（纳米）.1纳米＝10^－9米，那么100nm用科学记数法可以表示为（）

A . 0.1×10^-6米 B . 10×10^-7 米 C . 1×10^-6 米 D . 1×10^-7米

答案解析收藏纠错 + 选题
3. (2022七上·济阳期末) 下列哪组长度的三条线段能组成三角形?（）

A . 1cm、2cm、4cm B . 3cm、4cm、7cm C . 2cm、2cm、1cm D . 5cm、3cm、2cm

答案解析收藏纠错 + 选题
4. (2022七下·惠山期中) 如图，AB∥DE，BC∥EF，则∠E与∠B的关系一定成立的是（）

A . 互余 B . ∠E=2∠B C . 相等 D . 互补

答案解析收藏纠错 + 选题
5. (2022七下·惠山期中) 如图，若要使AD∥BC，则可以添加条件（）

A . ∠2＝∠3 B . ∠B＋∠BCD＝180° C . ∠1＝∠4 D . ∠1＝∠3

答案解析收藏纠错 + 选题
6. (2024七下·苏州工业园期中) 下列各式从左边到右边的变形，是因式分解且分解正确的是（）

A . （a＋1）（a－1）＝a²－1 B . a²－8a＋16＝（a－4）² C . a²－2a+4＝（a－2）² D . ab＋ac＋1＝a（b＋c）＋1

答案解析收藏纠错 + 选题
7. (2023七上·梁溪月考) 用一个容量为2GB（1GB=2¹⁰MB）的便携式优盘存储数码照片，若每张数码照片的文件大小都为16MB，则理论上可以存储的照片数是（）

A . 2¹⁰张 B . 2⁸张 C . 2⁷张 D . 2⁶张

答案解析收藏纠错 + 选题
8. (2022七下·惠山期中) 下列各式能用平方差公式计算的是（）

A . （－2x+y）（－2x－y） B . （2x+y）（x－2y） C . （x－2y）（－x+2y） D . （－2x+y）（－x+2y）

答案解析收藏纠错 + 选题
9. (2024七下·兰考期中) 我国古代数学名著《张邱建算经》中记载：“今有清酒一斗直粟十斗，醑酒一斗直粟三斗.今持粟三斛，得酒五斗，问清、醑酒各几何？”意思是：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子.现在拿30斗谷子，共换了5斗酒，问清、醑酒各几斗？如果设清酒x斗，醑酒y斗，那么可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七下·苏州工业园期中) 对于a、b两数定义@的一种运算：a@b=（a▪b）a⁺b（其中等式右边的▪和+是通常意义下的乘法与加法），则下列结论：
①若a=1，b=－2，则a@b=－ $\text{[math]}$ ； ②若（－1）@x=1，则x=1；③a@b=b@a；④当a、b互为相反数时，a@b的值总是等于1.其中正确的是（）

A . ①②④ B . ①③ C . ①③④ D . ②③

答案解析收藏纠错 + 选题

二、填空题

11. (2022八下·徐汇期末) 正五边形的内角和等于度.

答案解析收藏纠错 + 选题
12. (2022七下·惠山期中) 如图，已知∠ACP＝115°，∠B＝65°，则∠A＝.

答案解析收藏纠错 + 选题
13. (2022七下·惠山期中) 若 $\text{[math]}$ 是二元一次方程2x＋3y＝k的一个解，则k的值是.

答案解析收藏纠错 + 选题
14. (2024七下·苏州工业园期中) 多项式 $\text{[math]}$ 分解因式时所提取的公因式是.

答案解析收藏纠错 + 选题
15. (2024七下·宜春期中) 如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C平移的距离CC＇＝.

答案解析收藏纠错 + 选题
16. (2022七下·惠山期中) 若a^m＝9，aⁿ＝3，则a^m-n＝.

答案解析收藏纠错 + 选题
17. (2022七下·惠山期中) 已知关于x的代数式4x²+ax+9是完全平方式，则a=.

答案解析收藏纠错 + 选题
18. (2022七下·惠山期中) 如图，将三角形纸片ABC沿EF折叠，使得A点落在BC上点D处，连接DE，DF， $\text{[math]}$ .设 $\text{[math]}$ ， $\text{[math]}$ ，则α与β之间的数量关系是.

答案解析收藏纠错 + 选题

三、解答题

19. (2022七下·惠山期中) 计算或化简：
1. （1） $\text{[math]}$
2. （2） a² $\text{[math]}$ a⁴＋a⁸÷a²+（－2a²）³
3. （3）（a+1）²+a（3－a）；
4. （4）（m+1）² $\text{[math]}$ （m﹣1）².
答案解析收藏纠错 + 选题
20. (2022七下·惠山期中) 因式分解：
1. （1） mx²﹣my²；
2. （2） 2x²－8x+8.
答案解析收藏纠错 + 选题
21. (2022七下·惠山期中) 先化简，再求值：（x－2）²＋4（x－y）－（2y－1）² ，其中x＝4.85，y＝2.575.

答案解析收藏纠错 + 选题
22. (2022七下·惠山期中) 如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点.仅用无刻度的直尺完成下列作图.
1. （1）画出△ABC向右平移4个单位后的图形△A₁B₁C₁（注意标上字母）；
2. （2）画出△ABC的中线CD（注意标上字母）；
3. （3）画出满足△QBC与△ABC面积相等的一个格点Q（与点A不重合）.
答案解析收藏纠错 + 选题
23. (2022七下·南京期末) 如图，△ABC中，D为AC边上一点，过D作DE∥AB，交BC于E；F为AB边上一点，连接DF并延长，交CB的延长线于G，且∠DFA＝∠A.
1. （1）求证：DE平分∠CDF；
2. （2）若∠C＝80°，∠ABC＝60°，求∠G的度数.
答案解析收藏纠错 + 选题
24. (2022七下·惠山期中) 阅读以下材料：
若x²－4x＋y²－10y＋29=0，求x、y的值.
思路分析：一个方程求两个未知数显然不容易，考虑已知等式的特点，将其整理为两个完全平方式的和，利用其非负性转化成两个一元一次方程，进而求出x、y.
解：∵x²－4x＋y²－10y＋29=0，
∴（x²－4x+4）＋（y²－10y＋25）=0，
∴（x－2）²+（y－5）²=0，
∴x=2，y=5.
请你根据上述阅读材料解决下列问题：
1. （1）若m²＋2m＋n²－6n＋10＝0，则m+n= ；
2. （2）请你说明：无论x、y取何值，代数式x²－4xy＋5y²＋2y＋5的值一定是正数.
答案解析收藏纠错 + 选题
25. (2022七下·惠山期中) 数形结合是解决数学问题的一种重要思想方法，借助图形的直观性，可以帮助理解数学问题.
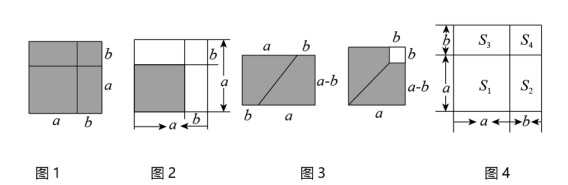
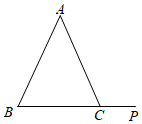
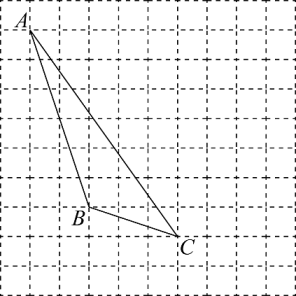
1. （1）请写出图1，图2，图3阴影部分的面积分别能解释的数学公式.
  
  图1：；图2：；图3：.
2. （2）其中，完全平方公式可以从“数”和“形”两个角度进行探究，并通过公式的变形或图形的转化可以解决很多数学问题.
  
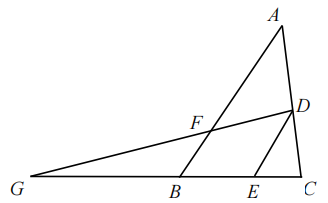
  例如：如图4，已知a+b＝3，ab＝1，求a²+b²的值.
  
  方法一：从“数”的角度
  
  解：∵a+b＝3，
  
  ∴（a+b）²＝9，即：a²+2ab+b²＝9，
  
  又∵ab＝1
  
  ∴a²+b²＝7.
  
  方法二：从“形”的角度
  
  解：∵a+b＝3，
  
  ∴S_大正方形=9，
  
  又∵ab＝1，
  
  ∴S₂＝S₃＝ab＝1，
  
  ∴S₁+S₄＝S_大正方形﹣S₂﹣S₃＝9﹣1﹣1＝7.即a²+b²＝7.
  若（5﹣x）▪（x﹣1）＝3，则（5﹣x）²+（x﹣1）²＝；
3. （3）如图，点C是线段AB上的一点，以AC，BC为边向两边作正方形，设AB＝10，两正方形的面积和S₁+S₂＝72，求图中阴影部分面积.
答案解析收藏纠错 + 选题
26. (2022七下·惠山期中) 引入概念1：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”.
引入概念2：从不等边三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形.若分成的两个小三角形中一个是满足有两个角相等的三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”.
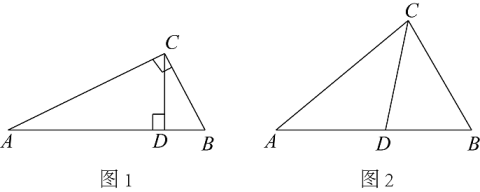
1. （1）如图1，在Rt△ABC中，∠ACB=90°，CD⊥AB，请写出图中两对“等角三角形”.
  ①；②.
2. （2）如图2，在△ABC中，CD为角平分线，∠A=40°，∠B=60°.请你说明CD是△ABC的等角分割线.
3. （3）在△ABC中，若∠A=40°，CD为△ABC的等角分割线，请你直接写出所有可能的∠B度数.
答案解析收藏纠错 + 选题