吉林省长春市长春新区2021-2022学年八年级下学期期末考...

更新时间：2022-09-07 浏览次数：70 类型：期末考试

一、单选题

1. 下列代数式中，属于分式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022七下·安庆期末) “ $\text{[math]}$ ”表示此类型的口罩能过滤空气中 $\text{[math]}$ 的粒径约为 $\text{[math]}$ 的非油性颗粒，其中 $\text{[math]}$ 用科学记数法表示为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 在平面直角坐标系中，点P的坐标为 $\text{[math]}$ ，那么点P在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
4. 把分式 $\text{[math]}$ 中的x，y的值同时扩大为原来的2倍，则分式的值（）

A . 不变 B . 扩大为原来的2倍 C . 扩大为原来的4倍 D . 缩小为原来的 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022八下·平阴期末) 如图，在四边形ABCD中，AB $\text{[math]}$ CD，要使四边形ABCD是平行四边形，下列添加的条件错误的是（）

A . AB＝CD B . BC＝AD C . ∠A＝∠C D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. 某同学这学期前四次数学测验的成绩依次为93、82、76和88，马上要进行第五次数学测验了，她这五次成绩的平均数能够达到或超过85分，那么，这次测验她的分数至少是（）

A . 83 B . 84 C . 85 D . 86

答案解析收藏纠错 + 选题
7. 如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处，易证四边形AECF是平行四边形．当∠BAE为（）度时，四边形AECF是菱形．

A . 30° B . 40° C . 45° D . 50°

答案解析收藏纠错 + 选题
8. (2021八下·内江期末) 在同一直角坐标系中，函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2022八下·和平期末) 当式子 $\text{[math]}$ 有意义时，实数 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
11. 在平面直角坐标系中，将直线 $\text{[math]}$ 沿着y轴向下平移3个单位长度，平移后的直线所对应的函数解析式为．

答案解析收藏纠错 + 选题
12. (2022八下·丰润期末) 在平面直角坐标系中，一次函数y=kx和y=-x+3的图象如图所示，则二元一次方程组 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
13. 如图，四边形ABCD是边长为 $\text{[math]}$ cm的菱形，其中对角线BD的长为2cm，则菱形ABCD的面积为 cm² ．

答案解析收藏纠错 + 选题
14. 在平面直角坐标系中，若点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 都在函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的大小关系是（用“＞”号连接）．

答案解析收藏纠错 + 选题

三、解答题

15. 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. 为丰富师生的体育文化生活，某中学决定组建足球社团，学校在商场购进A、B两种品牌的足球，购买A品牌足球花费了2000元，购买B品牌足球花费了2500元，且购买A品牌足球数量是购买B品牌足球数量的2倍，已知购买一个B品牌足球比购买一个A品牌足球多花30元，问购买一个B品牌的足球花费多少钱？

答案解析收藏纠错 + 选题
17. 图①、图②都是4×4的正方形网格，每个小正方形的顶点称为格点，点A、B均在格点上，仅用无刻度的直尺在下列网格中按要求作图．
1. （1）在图①中，画出一个以AB为边的四边形ABCD，使其是中心对称图形不是轴对称图形且边长均为无理数．
2. （2）在图②中，画出一个以线段AB为边的四边形ABMN，使其既是轴对称图形又是中心对称图形．
答案解析收藏纠错 + 选题
18. 如图，在△ABC中，AB＝AC，AD⊥BC于点D，过点B作AD的平行线交外角∠BAF的平分线于点E．求证：四边形ADBE是矩形．

答案解析收藏纠错 + 选题
19. 如图，在平面直角坐标系中，O为坐标原点，点A，B在函数 $\text{[math]}$ 的图象上（点A的纵坐标大于点B的纵坐标），点A的坐标为（2，4），过点A作AD⊥x轴于点D，过点B作BC⊥x轴于点C，连结OA，AB．
1. （1）求k的值．
2. （2）若CD＝2OD，求四边形OABC的面积．
答案解析收藏纠错 + 选题
20. 某校为了调查学生对环境保护知识的了解情况，从七、八两个年级各随机抽取50名学生进行了相关知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息：
a．八年级50名学生成绩的频数分布统计表如下：
成绩x
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
学生人数
5
14
15
13
3
b．八年级成绩在 $\text{[math]}$ 这一组的是：
71 71 72 72 73 75 75 75 76 77 77 78 79 79 79
c．七、八两个年级成绩的平均分、中位数、众数和方差如下．
年级
平均数
中位数
方差
七
74
73.8
122.3
八
74
n
89.2
根据以上信息，回答下列问题：
1. （1）表格中n＝．
2. （2）在此次测试中，某学生的成绩是74.5分，在他所属年级排在前20名，由表中数据可知该学生是年级的学生．（填“七”或“八”）
3. （3）根据以上信息，你认为七、八两个年级中，哪个年级学生了解环境保护知识的情况较好，请从两个方面说出你的判断依据．
答案解析收藏纠错 + 选题
21. 小明和小红分别从甲、乙两地沿同一条路同时出发，相向而行．小明从甲地到乙地，小红从乙地到甲地，小明和小红离甲地的距离y（千米）与时间x（小时）之间的函数图象如图所示，根据图中提供的信息，解答下列问题：
1. （1）小红出发后速度为千米/小时．
2. （2）求线段AB对应的函数表达式，写出自变量x的取值范围．
3. （3）当小红到达甲地时，小明距乙地还有多远？
答案解析收藏纠错 + 选题
22. 【阅读材料】如图①，在边长为4的正方形ABCD中，点E、F分别在边BC、CD上且∠EAF＝45°，连接EF，求△CEF的周长．
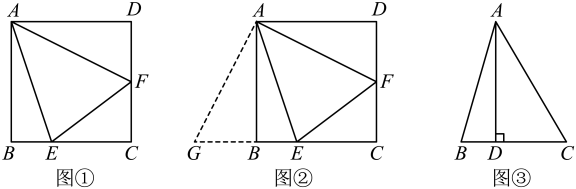
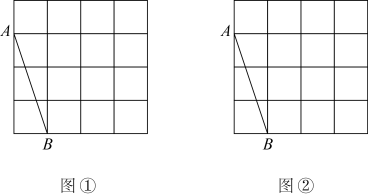
小明想到解决问题的方法如下：
如图②，延长CB至点G，使BG＝DF，通过证明 $\text{[math]}$ ，得到BE、DF、EF之间的关系，进而求出△CEF的周长．
1. （1）请按照小明的思路，帮助小明写出完整的求解过程．
2. （2）【方法应用】如图②，若BE＝1，求DF的长．
3. （3）【能力提升】如图③，在锐角△ABC中，∠BAC＝45°，AD⊥BC于点D．若BD＝1，AD＝4，则CD的长为．
答案解析收藏纠错 + 选题
23. 如图，在 $\text{[math]}$ 中，AB＝5，BC＝9， $\text{[math]}$ 的面积为36，动点P从A点出发，以1个单位长度的速度沿线段AD向终点D运动，同时动点Q从点B出发以3个单位长度的速度在BC间往返运动，当点P到达点D时，动点P、Q同时停止运动，连结PQ．设运动时间为t秒．
1. （1）直线AD与BC之间的距离是．
2. （2）当点Q从点C向点B运动时（点Q不与点B、C重合），设四边形ABQP的面积为S，求S与t之间的函数关系式，并写出自变量t的取值范围．
3. （3）当PQ⊥BC时，求t的值．
4. （4）当PQ平分 $\text{[math]}$ 的面积时，直接写出t的值．
答案解析收藏纠错 + 选题
24. 在平面直角坐标系中，函数 $\text{[math]}$ 的图象记作G（其中m为常数，且m≠0），点M坐标为 $\text{[math]}$ ，点N坐标为（3，1）．
1. （1）当图象过点N时，求m的值．
2. （2）在（1）的条件下．
  ①在给定的平面直角坐标系内画出图象G．
  ②当 $\text{[math]}$ 时，求函数值y的最大值和最小值．
3. （3）当图象G与线段MN只有一个交点时，直接写出m的取值范围．
答案解析收藏纠错 + 选题