 B .
B . 

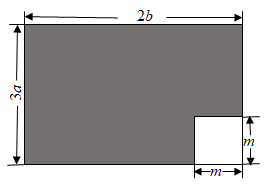
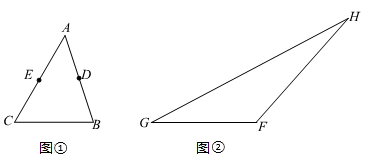
已知:∠AOB.
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
作法:如图,
①画射线O′A′;
②以O为圆心,任意长为半径画弧,交OA于点M,交OB于点N;
③以O′为圆心,OM长为半径画弧,交O′A′于点M′;
④以M′为圆心,MN长为半径画弧,交前弧于点N′;
⑤过N′作射线O′B′,则∠A′O′B′即为所求.
根据上述尺规作图过程,
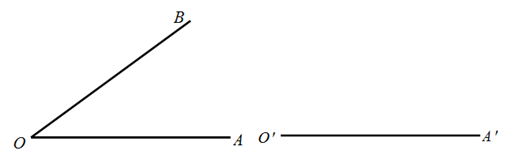
∵作图步骤③中,以O′为圆心,OM长为半径画弧,交O′A′于点M′,
∴OM= ▲ .
又∵作图步骤④中,以M′为圆心,MN长为半径画弧,交前弧于点N′,
∴ON= ▲ , MN= ▲ ,
∴△MON≌△M′O′N′, ( )(填推理的依据)
∴∠A′O′B′=∠AOB.

|
比较355 , 444 , 533的大小. 分析:小刚同学发现55,44,33都是11的倍数,于是把这三个数都转化为指数为11的幂,然后通过比较底数的方法,比较了这三个数的大小.解法如下: 解:∵ ∴ |
学习以上解题思路和方法,然后完成下题:
比较34040 , 43030 , 52020的大小.
|
已知am=3,an=5,求a3m+2n的值. 分析:小刚同学发现,这些已知的和所求的幂的底数都相同,于是逆用同底数幂和幂的乘方的公式,完成题目的解答.解法如下: 解:∵ ∴ |
学习以上解题思路和方法,然后完成下题:
已知am=2,an=3,求a2m+3n的值.
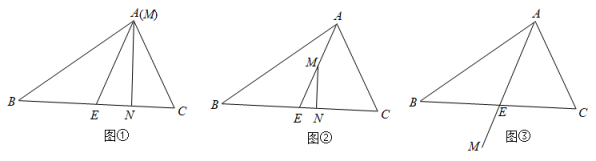
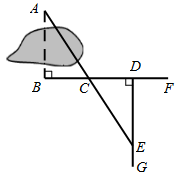
①依题意补全图形;
②若∠B=α°,∠ACB=β°,∠D=γ°,则∠AMC=°.
(用含α,β,γ的式子表示)