 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 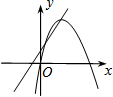
 B .
B .  C .
C . 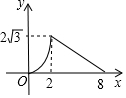 D .
D . 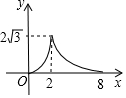
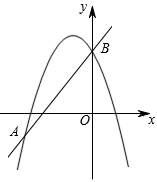
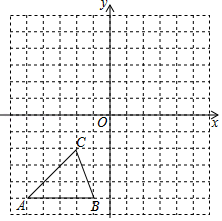
⑴画出△ABC以y轴为对称轴的对称图形△A1B1C1;
⑵以原点O为对称中心,画出△A1B1C1关原点O对称的△A2B2C2并写出点C2的坐标;
⑶以为旋转中心,把△A2B2C2顺时针旋转90°,得到△C2A3B3 .
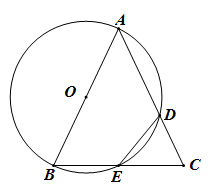
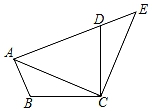
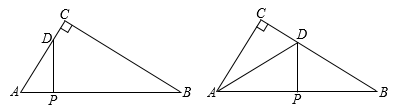
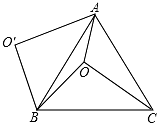
图1中,线段 的数量关系是,
的大小为;
把 绕点A顺时针方向旋转到如图2所示的位置,连接
判断
的形状,并说明理由;
把 绕点A在平面内自由旋转,若
,请求出
面积的最大值.