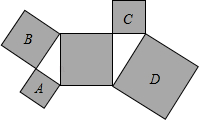
 B .
B .  C .
C .  D .
D . 






|
节目类型 |
人数 |
|
A |
20 |
|
B |
a |
|
C |
52 |
|
D |
80 |
|
E |
b |

请根据图中所给出的信息解答下列问题:

第二步:如图2,再一次折叠纸片,使点A落在EF上的N处,并使折痕经过点B,得到折痕BM,同时得到线段BN.

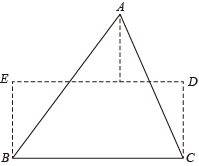
如图②,在△ABC中,AB、AC的垂直平分线分别交BC于点D、E,垂足分别为M,N,已知△ADE的周长为22,则BC的长为 .

①求证:△BCN≌△ACM.
②∠BDE的大小为 ▲ 度(用含β的代数式表示).