| x | 1 | 2 | 3 | 4 |
| y | ﹣3 | ﹣1 | 3 | 9 |

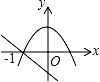 B .
B .  C .
C . 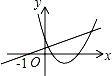 D .
D . 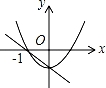
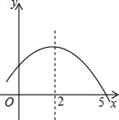
①b>0;
②若m= ,则3a+2c<0;
③若点M(x1 , y1),N(x2 , y2)在抛物线上,x1<x2 , 且x1+x2>1,则y1>y2;
④当a≤﹣1时,关于x的一元二次方程ax2+bx+c=1必有两个不相等的实数根.
其中正确的是 (填写序号).
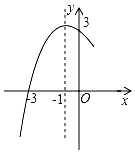


①求点E的坐标;
②直线y=2kx+k﹣ (k>0)与这条抛物线交于点M,N,连接ME,NE,判断ME,NE,MN之间的数量关系,并说明理由.