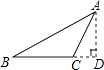
 B .
B .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 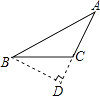
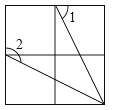

 B .
B .  C .
C .  D .
D . 






“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅”
请用学过的数学知识回答这个问题.

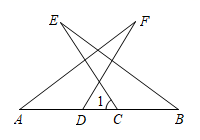



如果直角三角形ABC的两直角边长为3和4,则斜边上的高为.

①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.