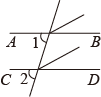
 B .
B . 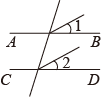 C .
C . 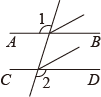 D .
D . 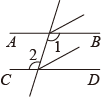
已知:的三个内角为
,
,
.
求证: .
证法1 | 证法2 |
如图1,延长 ∵ ∴
| 如图2,过点
又∵ ∴
|
下列说法正确的是( )
| 证明:如图,∵ ∵ ∴∠1=∠2,∴
|
已知该证明过程是正确的,则证明的真命题是( )

 B .
B .  C .
C .  D .
D . 

证明:∵ ,
( ① ),
∴ . 又∵
, ∴
∴∥
( ② ).
其中①②为解题依据,则下列描述正确的是( )

证明:∵()
∴∠CDA=90°,∠DAB=90°().
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴(),
∴DF∥AE().
已知:如图,∠1+∠2=180°,∠3+∠4=180°.
求证:AB∥EF .
证明:∵∠1+∠2=180°,
∴AB∥().
∵∠3+∠4=180°,
∴∥.
∴AB∥EF().

如图,已知
证明:∵ ∴ ∴ ∴ ∴ …… |
任务:
“依据1”:.
“依据2”:.